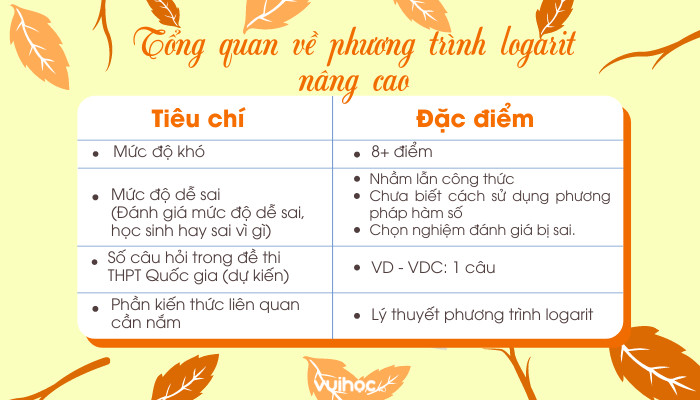
Để giải quyết các bài toán logarit phức tạp, việc nắm vững các Công Thức Logarit Nâng Cao là vô cùng quan trọng. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan và chi tiết về các công thức này, giúp bạn tự tin chinh phục mọi thử thách.
1. Tổng Quan Về Logarit
1.1. Định Nghĩa Logarit
Logarit cơ số a của một số b là số mũ mà ta cần nâng a lên để được b. Ký hiệu: loga(b) = x ⇔ ax = b
Trong đó:
- a là cơ số (a > 0, a ≠ 1)
- b là số thực dương
1.2. Các Dạng Phương Trình Logarit Thường Gặp
Phương trình logarit có nhiều dạng khác nhau, từ cơ bản đến phức tạp. Dưới đây là một số dạng thường gặp:
- Dạng cơ bản: loga(x) = b
- Dạng chứa ẩn ở cơ số: logx(a) = b
- Dạng phức tạp: Các phương trình kết hợp nhiều phép toán logarit, mũ, căn, và các hàm số khác.
2. Các Công Thức Logarit Nâng Cao
2.1. Công Thức Biến Đổi Cơ Bản
Đây là nền tảng để giải quyết các bài toán logarit.
- loga(b*c) = loga(b) + loga(c)
- loga(b/c) = loga(b) – loga(c)
- loga(bc) = c * loga(b)
- logan(b) = (1/n) * loga(b)
- loga(b) = 1 / logb(a) (Công thức đổi cơ số)
- aloga(b) = b
2.2. Các Công Thức Nâng Cao Hơn
Những công thức này thường được sử dụng trong các bài toán phức tạp hơn.
- Công thức đổi cơ số tổng quát: loga(b) = logc(b) / logc(a) (c > 0, c ≠ 1)
- Công thức mũ hóa: alogb(c) = clogb(a)
- loga(f(x)) = loga(g(x)) <=> f(x) = g(x) (với f(x), g(x) > 0)
3. Phương Pháp Giải Phương Trình Logarit Nâng Cao
3.1. Đưa Về Cùng Cơ Số
Đây là phương pháp cơ bản và quan trọng.
- Bước 1: Xác định cơ số chung.
- Bước 2: Sử dụng công thức đổi cơ số để đưa tất cả các logarit về cơ số chung.
- Bước 3: Giải phương trình thu được.
3.2. Đặt Ẩn Phụ
Phương pháp này giúp đơn giản hóa phương trình.
- Bước 1: Xác định biểu thức lặp lại trong phương trình.
- Bước 2: Đặt ẩn phụ cho biểu thức đó.
- Bước 3: Giải phương trình theo ẩn phụ.
- Bước 4: Thay lại để tìm nghiệm ban đầu.
3.3. Mũ Hóa
Sử dụng khi phương trình có cả logarit và mũ.
- Bước 1: Xác định cơ số của logarit.
- Bước 2: Mũ hóa cả hai vế của phương trình với cơ số đó.
- Bước 3: Giải phương trình thu được.
3.4. Sử Dụng Đồ Thị
Phương pháp này hữu ích khi không thể giải bằng các phương pháp đại số thông thường.
- Bước 1: Vẽ đồ thị của hai hàm số ở hai vế của phương trình.
- Bước 2: Tìm giao điểm của hai đồ thị. Hoành độ giao điểm là nghiệm của phương trình.
3.5. Kết Hợp Các Phương Pháp
Trong nhiều trường hợp, cần kết hợp nhiều phương pháp để giải quyết một bài toán.
4. Ví Dụ Minh Họa
Dưới đây là một số ví dụ minh họa cách áp dụng các công thức và phương pháp đã học để giải các bài toán logarit nâng cao.
5. Luyện Tập
Để nắm vững kiến thức và kỹ năng giải toán logarit, bạn cần luyện tập thường xuyên. Hãy tìm kiếm các bài tập tương tự và thử sức mình. Chúc bạn thành công!