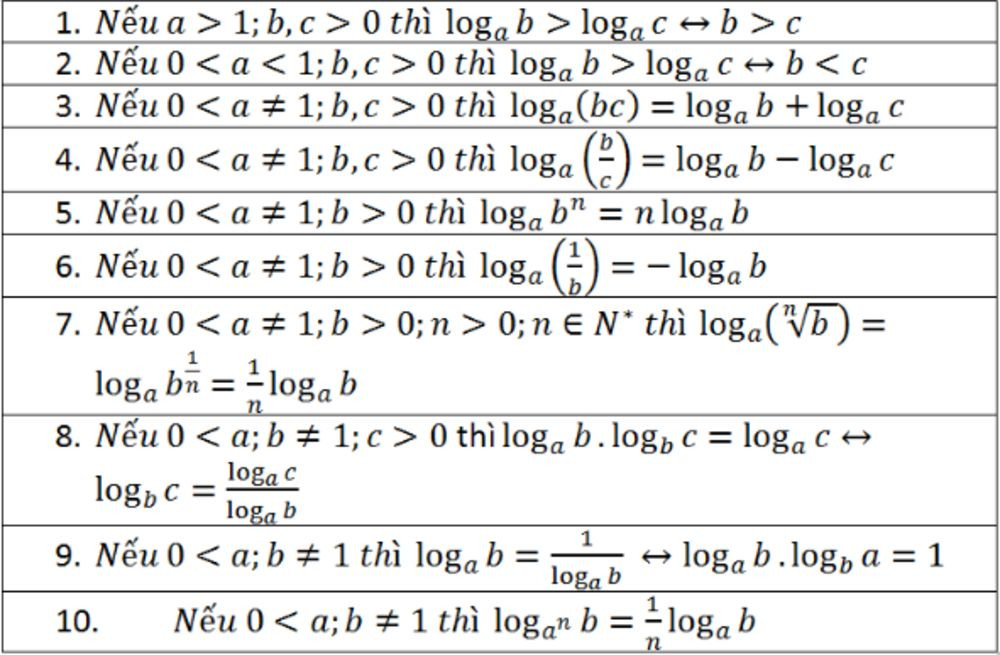Logarit là một phần kiến thức toán học quan trọng trong chương trình THPT, và nắm vững các Công Thức Logarit là điều kiện tiên quyết để giải quyết các bài tập và bài thi một cách hiệu quả. Bài viết này sẽ cung cấp một hệ thống đầy đủ và chi tiết về các công thức logarit, giúp học sinh dễ dàng ôn tập và áp dụng.
Logarit Là Gì?
Logarit là phép toán nghịch đảo của lũy thừa. Logarit của một số là số mũ mà cơ số (một giá trị cố định) cần được nâng lên để tạo thành số đó. Nói cách khác, logarit cho biết một số được lặp lại bao nhiêu lần trong phép nhân.
Ví dụ:
- 2³ = 8
- log₂8 = 3 (Logarit cơ số 2 của 8 là 3)
Các Tính Chất Quan Trọng Của Logarit
Các tính chất của logarit là nền tảng để biến đổi và giải các bài toán liên quan đến công thức logarit. Dưới đây là một số tính chất cần nhớ:
- logₐ1 = 0 (với a > 0, a ≠ 1)
- logₐa = 1 (với a > 0, a ≠ 1)
- logₐ(xy) = logₐx + logₐy (với a > 0, a ≠ 1, x > 0, y > 0)
- logₐ(x/y) = logₐx – logₐy (với a > 0, a ≠ 1, x > 0, y > 0)
- logₐ(xⁿ) = n*logₐx (với a > 0, a ≠ 1, x > 0)
Hình ảnh minh họa các tính chất cơ bản của logarit, bao gồm logarit của tích, thương, lũy thừa và các trường hợp đặc biệt với cơ số và đối số.
Tổng Hợp Các Công Thức Logarit Chi Tiết Nhất
Dưới đây là bảng tổng hợp đầy đủ các công thức logarit, bao gồm công thức cơ bản, công thức lũy thừa, công thức liên quan đến các phép toán và công thức đổi cơ số.
1. Các Công Thức Logarit Cơ Bản
- a^(logₐx) = x
- logₐ(a^x) = x
Hình ảnh minh họa các công thức logarit cơ bản, nhấn mạnh vào mối quan hệ giữa logarit và lũy thừa.
Hình ảnh minh họa bảng tổng hợp các công thức logarit thường gặp, dễ dàng tra cứu và áp dụng.
2. Công Thức Lũy Thừa Logarit
- logₐ(b^α) = α*logₐb
Hình ảnh minh họa công thức logarit của một lũy thừa, thể hiện rõ cách đưa số mũ ra ngoài dấu logarit.
3. Công Thức Logarit và Các Phép Toán
- logₐ(xy) = logₐx + logₐy
- logₐ(x/y) = logₐx – logₐy
Hình ảnh minh họa các công thức biến đổi logarit của tích và thương, làm nổi bật tính chất phân rã của logarit.
4. Công Thức Đổi Cơ Số Logarit
- logᵇx = (logₐx) / (logₐb)
Hình ảnh minh họa công thức đổi cơ số, giúp tính toán logarit với cơ số bất kỳ thông qua một cơ số trung gian.
5. Công Thức Đạo Hàm Logarit
a. Đạo Hàm Logarit Hàm Cơ Bản
- (logₐx)’ = 1 / (x*ln(a))
- (ln(x))’ = 1/x
b. Đạo Hàm Logarit Hàm Hợp
- (logₐu(x))’ = u'(x) / (u(x)*ln(a))
- (ln(u(x)))’ = u'(x) / u(x)
Hình ảnh minh họa các công thức đạo hàm của hàm logarit cơ bản và hàm hợp, quan trọng trong giải tích.
Các Quy Tắc Quan Trọng Khi Sử Dụng Công Thức Logarit
Để áp dụng các công thức logarit một cách chính xác và hiệu quả, cần nắm vững các quy tắc sau:
- Quy tắc logarit của lũy thừa: logₐ(b^α) = α*logₐb (a, b > 0, a ≠ 1)
- Quy tắc logarit của một tích: logₐ(xy) = logₐx + logₐy (a > 0, a ≠ 1, x, y > 0)
Lưu Ý Quan Trọng Khi Học Và Sử Dụng Công Thức Logarit
Khi học và áp dụng các công thức logarit, cần lưu ý những điều sau:
- Phân biệt hàm mũ và logarit: Hàm mũ có dạng y = a^x, trong khi hàm logarit có dạng y = logₐx.
- Ghi nhớ các thành phần của công thức logarit: Bao gồm cơ số (a), đối số (x) và giá trị logarit (y).
- Phân biệt các loại logarit: Logarit thập phân (cơ số 10), logarit tự nhiên (cơ số e), và logarit cơ số bất kỳ.
Hình ảnh tổng hợp các lưu ý quan trọng khi học và sử dụng công thức logarit, giúp tránh sai sót và hiểu sâu hơn về bản chất.
Để học thuộc và sử dụng thành thạo các công thức logarit, hãy:
- Nắm vững kiến thức cơ bản về logarit và các tính chất liên quan.
- Luyện tập giải nhiều bài tập từ cơ bản đến nâng cao.
- Trao đổi và thảo luận với bạn bè, thầy cô để hiểu rõ hơn về các khái niệm và ứng dụng.
- Tham khảo các tài liệu, diễn đàn, và website uy tín để mở rộng kiến thức.
Hy vọng với những kiến thức và công thức logarit được trình bày chi tiết trong bài viết này, các bạn học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến logarit. Chúc các bạn thành công!