Kiến Thức Cần Nhớ Về Diện Tích Hình Tròn và Hình Quạt Tròn
Công Thức Tính Diện Tích Hình Tròn
Diện tích hình tròn (S) với bán kính R được tính theo công thức quen thuộc:
S = πR²
Công Thức Tính Diện Tích Hình Quạt Tròn
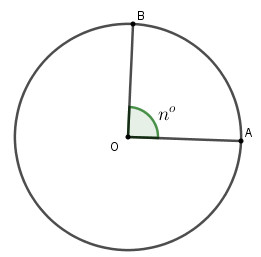
Để tính diện tích hình quạt tròn, chúng ta cần biết bán kính (R) và số đo cung (n°) của hình quạt đó. Công thức tính diện tích hình quạt tròn như sau:
S = (πR²n)/360 hay S = (lR)/2
Trong đó:
- S là diện tích hình quạt tròn.
- R là bán kính của hình tròn.
- n là số đo độ của cung tròn.
- l là độ dài cung tròn.
Hình ảnh minh họa hình quạt tròn với các yếu tố bán kính (R), cung tròn và góc ở tâm (n°), giúp người đọc hình dung rõ ràng hơn về khái niệm và công thức tính diện tích.
Các Dạng Bài Tập Thường Gặp Về Diện Tích Hình Quạt
Dạng 1: Tính Diện Tích Hình Tròn, Hình Quạt Tròn và Các Yếu Tố Liên Quan
Phương pháp:
Áp dụng trực tiếp các công thức tính diện tích hình tròn và hình quạt tròn đã nêu ở trên.
Ví dụ: Cho hình quạt tròn có bán kính R = 5 cm, số đo cung n = 60°. Tính diện tích hình quạt tròn đó.
Giải: Áp dụng công thức S = (πR²n)/360, ta có S = (π * 5² * 60)/360 = (25π)/6 ≈ 13.09 cm².
Dạng 2: Bài Toán Tổng Hợp Về Diện Tích Hình Quạt Tròn
Phương pháp:
Trong các bài toán phức tạp hơn, bạn cần sử dụng linh hoạt các kiến thức về hình học để tìm ra góc ở tâm, bán kính, hoặc độ dài cung tròn. Sau đó, áp dụng Công Thức Diện Tích Hình Quạt tròn để giải bài toán.
Ví dụ: Một hình tròn có bán kính 6cm. Một hình quạt tròn của hình tròn này có diện tích 12π cm². Tính số đo cung của hình quạt tròn.
Giải: Sử dụng công thức S = (πR²n)/360, ta có 12π = (π * 6² * n)/360. Giải phương trình này, ta tìm được n = (12π * 360) / (π * 36) = 120°.
Bài Tập Vận Dụng Tính Diện Tích Hình Quạt Tròn
Câu 1. Một hình tròn có đường kính 10cm. Tính diện tích của hình tròn đó.
Lời giải:
Bán kính của hình tròn là R = 10/2 = 5 cm.
Diện tích của hình tròn là S = πR² = π * 5² = 25π cm².
Câu 2. Tính độ dài cung 45° của một đường tròn có bán kính 8 cm.
Lời giải:
Độ dài cung tròn l = (πRn)/180 = (π 8 45)/180 = 2π cm.
Câu 3. Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC ⊥ OA. Biết độ dài đường tròn (O) là 6π cm. Tính độ dài cung lớn BC.
Lời giải:
Hình ảnh minh họa đường tròn (O), dây BC vuông góc với OA tại trung điểm M, giúp người đọc hình dung bài toán và áp dụng kiến thức hình học để giải.
Vì độ dài đường tròn là 6π nên 6π = 2πR => R = 3 cm.
Xét tứ giác ABOC có hai đường chéo AO ⊥ BC tại M là trung điểm mỗi đường nên tứ giác ABOC là hình thoi.
Suy ra OB = OC = AB => ΔABO đều => widehat {AOB} = 60° => widehat {BOC} = 120°
Suy ra số đo cung lớn BC là 360° – 120° = 240°
Độ dài cung lớn BC là l = (π 3 240)/180 = 4π cm.
Câu 4. Cho đường tròn (O, 6 cm), đường kính AB. Điểm M ∈ (O) sao cho widehat {BAM} = 30°. Tính diện tích hình quạt AOM.
Lời giải:
Hình ảnh minh họa đường tròn tâm O, đường kính AB và điểm M trên đường tròn tạo thành góc BAM = 30 độ, giúp người đọc dễ dàng hình dung và giải bài toán tính diện tích hình quạt AOM.
Ta có widehat {AOM} = 2 widehat{ABM} = 2 (90° – 30°) = 120°.
Vậy diện tích hình quạt AOM là S = (π 6² 120)/360 = 12π cm².
Câu 5. Cho đường tròn (O) đường kính AB = 8 cm. Điểm C ∈ (O) sao cho widehat {ABC} = 60°. Tính diện tích hình viên phân AC.
Lời giải:
Hình ảnh minh họa hình viên phân AC được tạo bởi cung AC và dây AC trong đường tròn (O), giúp người đọc hiểu rõ hơn về hình dạng cần tính diện tích.
widehat {AOC} = 2 widehat {ABC} = 2 60° = 120° => S_{qAOC} = (πR².120)/360 = (πR²)/3
Xét ΔAOC có widehat {AOC} = 120° và OA = OC = R nên tam giác AOC cân tại O.
Kẻ OH ⊥ AC. Ta có OH = R.cos(60°) = R/2 => S_{AOC} = (1/2)AC.OH = (1/2)R.sin(60°).R/2 = (√3/8)R²
Diện tích hình viên phân AC là: S_{qAOC} – S_{AOC} = (πR²)/3 – (√3/8)R² = ((8π – 3√3)/24)R² = ((8π – 3√3)/24) 8² = (8π – 3√3) 8 / 3 cm².
Câu 6. Cho đường tròn (O) đường kính AB = 4√2 cm. Điểm C ∈ (O) sao cho widehat {ABC} = 45°. Tính diện tích hình giới hạn bởi đường tròn (O) và AC, BC.
Lời giải:
Hình ảnh minh họa đường tròn (O) với tam giác ABC nội tiếp, giúp người đọc hình dung bài toán và xác định vùng cần tính diện tích.
Diện tích hình tròn (O) là: S_{(O)} = πR² = π(2√2)² = 8π cm².
Ta có góc widehat {ACB} là góc nội tiếp chắn nửa đường tròn => widehat {ACB} = 90°
=> widehat {BAC} = 90° – widehat {CBA} = 90° – 45° = 45°.
Tam giác ABC vuông cân tại C => AC = BC.
S_{ABC} = (1/2)AC.BC = (1/2)AC²
AC = AB.sin(45°) = 4√2 * (√2/2) = 4 cm
=> S_{ABC} = (1/2) * 4² = 8 cm².
Diện tích hình giới hạn bởi đường tròn (O) và AC, BC là:
(1/2)S_{(O)} – S_{ABC} = (1/2) * 8π – 8 = 4π – 8 cm².
Câu 7. Tại một vòng xoay ngã tư, người ta cần làm các bồn trồng hoa như hình vẽ. Em hãy tính phần diện tích của 1 bồn hoa (phần được tô đậm). Biết rằng bán kính của vòng tròn lớn là 9m, vòng tròn nhỏ là 4m, số đo cung tròn đó là 72°. (làm tròn đến hàng phần mười)
Lời giải:
Diện tích hình quạt tròn lớn là: (π 9² 72)/360 = 16.2π m²
Diện tích hình quạt tròn nhỏ là: (π 4² 72)/360 = 3.2π m²
Diện tích phần bồn hoa là: 16.2π – 3.2π = 13π ≈ 40.8 m²
Câu 8. Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh xe sau có đường kính là 1,824m và bánh xe trước có đường kính là 96cm. Hỏi khi bánh xe sau lăn được 15 vòng thì bánh xe trước lăn được mấy vòng?
Lời giải:
Ta có: 96cm = 0,96m
Chu vi bánh xe sau là: 1,824π (m)
Chu vi bánh xe trước là: 0,96π (m)
Khi bánh xe sau lăn được 15 vòng thì quãng đường đi được là:
1,824π * 15 = 27,36π (m)
Khi đó số vòng lăn của bánh trước là: 27,36π / 0,96π = 28,5 vòng.