Chuyển động ném ngang là một dạng chuyển động phức tạp, kết hợp giữa chuyển động thẳng đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng. Hiểu rõ các công thức và ứng dụng của nó giúp giải quyết nhiều bài toán vật lý và các tình huống thực tế.
1. Phân Tích Chuyển Động Ném Ngang
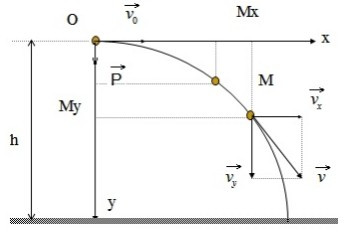
Để khảo sát chuyển động ném ngang, ta cần:
- Chọn hệ trục tọa độ: Ox nằm ngang theo hướng vận tốc ban đầu, Oy thẳng đứng hướng xuống theo gia tốc trọng trường.
- Gốc thời gian: Lúc vật bắt đầu được ném.
Chuyển động ném ngang có thể được phân tích thành hai thành phần:
- Theo phương Ox: Chuyển động thẳng đều với vận tốc không đổi.
- Theo phương Oy: Chuyển động rơi tự do với gia tốc trọng trường g.
Minh họa chuyển động ném ngang, thể hiện rõ sự phân tích thành hai thành phần chuyển động độc lập: chuyển động thẳng đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng.
Các phương trình chuyển động:
- Phương Ox:
- Vận tốc: $v_x = v_0$ (vận tốc ban đầu)
- Tọa độ: $x = v_0t$
- Phương Oy:
- Vận tốc: $v_y = gt$
- Tọa độ: $y = frac{1}{2}gt^2$
Phương trình chuyển động tổng quát:
- $x = v_0t$
- $y = frac{1}{2}gt^2$
2. Các Công Thức Quan Trọng
a) Quỹ đạo của vật:
Từ phương trình $x = v_0t$, suy ra $t = frac{x}{v_0}$. Thay vào phương trình $y = frac{1}{2}gt^2$, ta được:
$y = frac{g}{2v_0^2}x^2$
Đây là phương trình của một parabol, cho thấy quỹ đạo của vật ném ngang là một đường parabol.
b) Thời gian chuyển động:
Thời gian chuyển động của vật ném ngang phụ thuộc vào độ cao ban đầu (h) và gia tốc trọng trường (g):
$t = sqrt{frac{2h}{g}}$
c) Tầm ném xa:
Tầm ném xa (L) là khoảng cách vật đi được theo phương ngang từ lúc ném đến lúc chạm đất:
$L = v_0t = v_0sqrt{frac{2h}{g}}$
Biểu diễn trực quan công thức tầm ném xa, nhấn mạnh vai trò của vận tốc ban đầu $v_0$, độ cao $h$ và gia tốc trọng trường $g$.
3. Thí Nghiệm Kiểm Chứng
Thí nghiệm với hai viên bi, một viên được ném ngang và một viên rơi tự do đồng thời, chứng minh rằng thời gian rơi của cả hai là như nhau, chỉ phụ thuộc vào độ cao.
Mô tả thí nghiệm kiểm chứng chuyển động ném ngang, làm rõ sự đồng thời chạm đất của hai vật: một vật ném ngang và một vật rơi tự do từ cùng độ cao.
4. Ứng Dụng Thực Tế
Chuyển động ném ngang xuất hiện trong nhiều hoạt động hàng ngày, ví dụ như:
- Ném bóng rổ.
- Bắn pháo hoa.
- Sự di chuyển của các vật thể trong các trò chơi.
Hình ảnh minh họa các ứng dụng thực tế của chuyển động ném ngang trong các hoạt động thể thao và giải trí, tăng tính hấp dẫn và dễ hiểu.
5. Bài Tập Vận Dụng
Bài 1: Một vật được ném ngang từ độ cao 45m, vận tốc ban đầu 20m/s. Tính tầm ném xa và vận tốc khi chạm đất.
Giải:
- Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 45}{10}} = 3s$
- Tầm ném xa: $L = v_0t = 20 cdot 3 = 60m$
- Vận tốc theo phương ngang: $v_x = 20m/s$
- Vận tốc theo phương dọc: $v_y = gt = 10 cdot 3 = 30m/s$
- Vận tốc khi chạm đất: $v = sqrt{v_x^2 + v_y^2} = sqrt{20^2 + 30^2} = sqrt{1300} approx 36.06 m/s$
Bài 2: Một máy bay bay ngang ở độ cao 500m với vận tốc 180km/h, thả một gói hàng cứu trợ. Hỏi gói hàng rơi cách vị trí thả bao xa?
Giải:
- Đổi vận tốc: $180 km/h = 50 m/s$
- Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 500}{10}} = 10s$
- Tầm ném xa: $L = v_0t = 50 cdot 10 = 500m$
Bài 3: Từ một sân thượng cao 20m, một người ném ngang một hòn sỏi với vận tốc ban đầu 4m/s. Tính tầm xa của hòn sỏi và vận tốc của nó khi chạm đất.
Giải:
- Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 20}{10}} = 2s$
- Tầm xa: $L = v_0t = 4 cdot 2 = 8m$
- Vận tốc theo phương ngang: $v_x = 4m/s$
- Vận tốc theo phương dọc: $v_y = gt = 10 cdot 2 = 20m/s$
- Vận tốc khi chạm đất: $v = sqrt{v_x^2 + v_y^2} = sqrt{4^2 + 20^2} = sqrt{416} approx 20.4 m/s$
Hiểu và vận dụng thành thạo các Công Thức Chuyển động Ném Ngang giúp bạn giải quyết các bài toán vật lý liên quan và ứng dụng vào thực tiễn một cách hiệu quả.