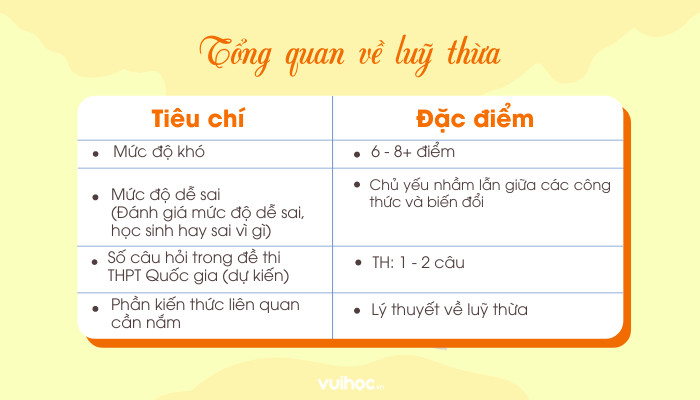
Lũy thừa là một phần kiến thức quan trọng trong chương trình Toán THPT, đặc biệt là các bài toán liên quan đến “Cộng Lũy Thừa” hay “lũy thừa cùng cơ số”. Để nắm vững dạng toán này và đạt điểm cao trong các kỳ thi, chúng ta cần hệ thống lại kiến thức và luyện tập thật kỹ.
1. Tổng Quan Về Lũy Thừa
1.1. Định Nghĩa Lũy Thừa
Lũy thừa là phép toán thực hiện trên hai số, gọi là cơ số (a) và số mũ (b). Kết quả của phép toán lũy thừa là tích của b thừa số a nhân với nhau. Kí hiệu: ab (đọc là a mũ b hoặc lũy thừa bậc b của a).
Ví dụ: 23 = 2 2 2 = 8
Phép toán ngược của lũy thừa là phép khai căn.
1.2. Phân Loại Lũy Thừa
Trong chương trình THPT, chúng ta làm quen với ba dạng lũy thừa chính:
- Lũy thừa với số mũ nguyên: an = a a … * a (n thừa số a), với n là số nguyên.
- a0 = 1 (a khác 0)
- a-n = 1/an (a khác 0)
- Lũy thừa với số mũ hữu tỉ: ar = am/n = n√am, với a > 0, r là số hữu tỉ (m ∈ Z, n ∈ N, n ≥ 2).
- Lũy thừa với số mũ thực: aα = lim (n→+∞) arn, với a > 0, α là số vô tỉ, rn là dãy số hữu tỉ thỏa mãn lim (n→+∞) rn = α.
Ví dụ:
1.3. Tính Chất Và Công Thức Lũy Thừa Cơ Bản
Nắm vững các tính chất lũy thừa là nền tảng để giải quyết các bài toán “cộng lũy thừa” và “lũy thừa cùng cơ số”.
Tính chất về đẳng thức:
- am * an = am+n
- am / an = am-n (a ≠ 0)
- (am)n = am*n
- (a b)m = am bm
- (a/b)m = am / bm (b ≠ 0)
Tính chất về bất đẳng thức:
So sánh cùng cơ số:
- Nếu a > 1: am > an <=> m > n
- Nếu 0 < a < 1: am > an <=> m < n
So sánh cùng số mũ:
- Với n > 0: a > b > 0 => an > bn
- Với n < 0: a > b > 0 => an < bn
Bảng công thức lũy thừa:
Lũy thừa của số e:
Số e ≈ 2.718 là cơ số của logarit tự nhiên (ln). Hàm e mũ, ký hiệu ex, thỏa mãn đẳng thức: ex+y = ex * ey.
Hàm lũy thừa với số mũ thực:
ax = ex*lna, với a > 0 và x là số thực.
2. Lũy Thừa Cùng Cơ Số
2.1. Định Nghĩa
Lũy thừa cùng cơ số là các lũy thừa có phần cơ số giống nhau (ax, ay, … với a là một số thực hoặc biểu thức).
2.2. Các Phép Tính Với Lũy Thừa Cùng Cơ Số
Các phép tính cơ bản khi làm việc với lũy thừa cùng cơ số:
- Nhân hai lũy thừa cùng cơ số: Giữ nguyên cơ số, cộng các số mũ. am * an = am+n
- Chia hai lũy thừa cùng cơ số: Giữ nguyên cơ số, trừ các số mũ. am / an = am-n (a ≠ 0)
3. Bài Tập Luyện Tập
Để thành thạo dạng toán “cộng lũy thừa”, “lũy thừa cùng cơ số”, cần luyện tập thường xuyên. Hãy tìm kiếm các bài tập từ cơ bản đến nâng cao và áp dụng các công thức, tính chất đã học để giải. Chú ý đến việc biến đổi các biểu thức để đưa về dạng lũy thừa cùng cơ số trước khi thực hiện các phép toán.
Chúc các bạn học tốt và chinh phục thành công các bài toán về lũy thừa!