Dao động của con lắc lò xo là một hiện tượng vật lý thú vị và quan trọng, đặc biệt trong chương trình Vật lý lớp 12. Hiểu rõ về Cơ Năng Của Con Lắc Lò Xo Dao động điều Hòa không chỉ giúp bạn giải quyết các bài tập mà còn cung cấp cái nhìn sâu sắc về bản chất của dao động. Bài viết này sẽ trình bày chi tiết về cơ năng của con lắc lò xo, các yếu tố ảnh hưởng và bài tập vận dụng.
1. Dao Động Điều Hòa của Con Lắc Lò Xo
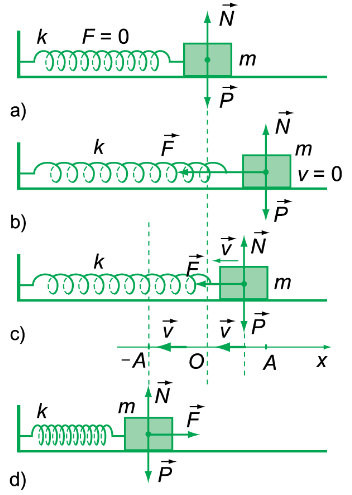
Để hiểu về cơ năng, trước tiên cần nắm vững về dao động điều hòa của con lắc lò xo. Xét một con lắc lò xo gồm vật nhỏ khối lượng m gắn vào lò xo có độ cứng k.
- Vị trí cân bằng: Là vị trí lò xo không biến dạng.
- Khi kéo vật ra khỏi vị trí cân bằng và buông tay, vật sẽ dao động quanh vị trí cân bằng.
Để khảo sát dao động, ta chọn trục tọa độ x và xét vật ở li độ x. Lực đàn hồi của lò xo là F = -kx. Theo định luật II Newton:
- F = ma = -kx
- Đặt ω² = k/m, ta có phương trình: a + ω²x = 0
Từ đó suy ra phương trình dao động điều hòa của con lắc lò xo:
Các thông số quan trọng:
- Tần số góc: ω = √(k/m)
- Chu kỳ: T = 2π/ω = 2π√(m/k)
- Lực kéo về: F = -kx = -mω²x (luôn hướng về vị trí cân bằng)
2. Năng Lượng Của Con Lắc Lò Xo
Năng lượng của con lắc lò xo bao gồm động năng và thế năng.
2.1. Động Năng
Động năng của con lắc lò xo được tính bằng công thức:
- Wd = (1/2)mv², trong đó m là khối lượng của vật và v là vận tốc.
2.2. Thế Năng
Thế năng của con lắc lò xo (thế năng đàn hồi) được tính bằng công thức:
- Wt = (1/2)kx², trong đó k là độ cứng của lò xo và x là li độ của vật.
2.3. Cơ Năng và Sự Bảo Toàn Cơ Năng
Cơ năng của con lắc lò xo là tổng của động năng và thế năng:
- W = Wd + Wt = (1/2)mv² + (1/2)kx² = (1/2)kA² = (1/2)mω²A² = const
Trong đó A là biên độ dao động.
Đặc điểm quan trọng:
- Cơ năng của con lắc lò xo tỉ lệ thuận với bình phương của biên độ dao động.
- Nếu bỏ qua ma sát, cơ năng của con lắc lò xo được bảo toàn.
2.4. Con Lắc Lò Xo Thẳng Đứng
Đối với con lắc lò xo thẳng đứng, cần lưu ý thêm một số yếu tố:
- Độ biến dạng của lò xo tại vị trí cân bằng: Δl = mg/k
- Chu kỳ dao động: T = 2π√(Δl/g)
- Chiều dài lò xo tại vị trí cân bằng: lCB = l0 + Δl (với l0 là chiều dài ban đầu)
- Chiều dài cực đại và cực tiểu: lmax = l0 + Δl + A và lmin = l0 + Δl – A
- Lực đàn hồi cực đại và cực tiểu: Fmax = k(Δl + A) và Fmin = k(Δl – A) (nếu A < Δl) hoặc Fmin = 0 (nếu A ≥ Δl)
3. Công Thức Tính Cơ Năng
Cơ năng của con lắc lò xo là một đại lượng không đổi (khi bỏ qua ma sát) và phụ thuộc vào bình phương biên độ dao động.
Công thức tính cơ năng:
- W = (1/2)kA²
- W = (1/2)mω²A²
4. Bài Tập Vận Dụng
Để hiểu rõ hơn về cơ năng của con lắc lò xo, hãy xem xét một số ví dụ sau:
Ví dụ 1: Một con lắc lò xo có độ cứng k = 100 N/m và biên độ A = 0.1 m. Tính động năng của con lắc khi vật cách vị trí cân bằng 7 cm.
Giải:
- Thế năng tại x = 0.07 m là Wt = (1/2)kx² = (1/2)(100)(0.07)² = 0.245 J
- Cơ năng của con lắc là W = (1/2)kA² = (1/2)(100)(0.1)² = 0.5 J
- Động năng là Wd = W – Wt = 0.5 – 0.245 = 0.255 J
Ví dụ 2: Một con lắc lò xo nằm ngang có độ cứng k = 100 N/m dao động điều hòa với động năng cực đại là 0.5 J. Tính biên độ dao động.
Giải:
- Động năng cực đại bằng cơ năng: W = 0.5 J
- Ta có W = (1/2)kA², suy ra A = √(2W/k) = √(20.5/100) = 0.1 m*
Ví dụ 3: Tìm tần số dao động của vật biết khoảng thời gian ngắn nhất giữa 2 lần động năng bằng thế năng là 0,05s.
Giải:
- Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là T/4 = 0,05s
- => T = 0,2s
- Tần số dao động của vật là f = 1/T = 5Hz
Ví dụ 4: Tìm li độ của vật khi động năng của lò xo gấp đôi thế năng biết con lắc dao động điều hòa với biên độ A?
Giải:
- Wđ = 2Wt
- W = Wđ + Wt = 3Wt
- 1/2kA² = 3 * 1/2kx²
- => x = ± A/√3
5. Bài Tập Trắc Nghiệm
Để củng cố kiến thức, hãy thử sức với các câu hỏi trắc nghiệm sau:
Câu 1: Cơ năng của con lắc lò xo tỉ lệ thuận với:
A. Biên độ dao động
B. Bình phương biên độ dao động
C. Tần số dao động
D. Khối lượng vật nặngĐáp án: B
Câu 2: Một con lắc lò xo có độ cứng 100 N/m và khối lượng 0.1 kg dao động điều hòa. Tần số góc của dao động là:
A. 10 rad/s
B. 100 rad/s
C. 1 rad/s
D. 0.1 rad/sĐáp án: A
Câu 3: Khi động năng của con lắc lò xo bằng thế năng, li độ của vật bằng bao nhiêu so với biên độ A?
A. A/2
B. A/√2
C. A/3
D. A/√3Đáp án: B
Kết Luận
Hiểu rõ về cơ năng của con lắc lò xo dao động điều hòa là rất quan trọng để nắm vững kiến thức Vật lý lớp 12 và giải quyết các bài tập liên quan. Bài viết này đã trình bày chi tiết về các khái niệm, công thức và ví dụ minh họa, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập. Chúc các bạn học tốt!