Tam giác đồng dạng là một chủ đề quan trọng trong chương trình Toán học, đặc biệt là ở lớp 9 và trong các kỳ thi tuyển sinh vào lớp 10. Việc nắm vững các phương pháp Cm 2 Tam Giác đồng Dạng không chỉ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả mà còn xây dựng nền tảng tư duy logic vững chắc. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về các cách cm 2 tam giác đồng dạng thường gặp, kèm theo ví dụ minh họa và hướng dẫn giải chi tiết.
Các Trường Hợp Đồng Dạng Của Tam Giác
Để cm 2 tam giác đồng dạng, chúng ta có ba trường hợp cơ bản sau:
-
Trường hợp cạnh – cạnh – cạnh (c-c-c): Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Xét hai tam giác ∆ABC và ∆DEF, nếu AB/DE = BC/EF = AC/DF thì ∆ABC ~ ∆DEF (c-c-c).
-
Trường hợp cạnh – góc – cạnh (c-g-c): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Xét hai tam giác ∆ABC và ∆DEF, nếu AB/DE = AC/DF và góc BAC = góc EDF thì ∆ABC ~ ∆DEF (c-g-c).
-
Trường hợp góc – góc (g-g): Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Xét hai tam giác ∆ABC và ∆DEF, nếu góc ABC = góc DEF và góc BAC = góc EDF thì ∆ABC ~ ∆DEF (g-g).
Các Trường Hợp Đồng Dạng Đặc Biệt Của Tam Giác Vuông
Đối với tam giác vuông, việc cm 2 tam giác đồng dạng trở nên đơn giản hơn nhờ các trường hợp đặc biệt:
- Cạnh huyền – cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
- Hai cạnh góc vuông: Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
- Góc nhọn: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Các Dạng Bài Tập Và Phương Pháp Chứng Minh Tam Giác Đồng Dạng
Dạng 1: Sử Dụng Hệ Thức Để Chứng Minh Tam Giác Đồng Dạng
Đây là dạng bài tập phổ biến, yêu cầu học sinh sử dụng các hệ thức về cạnh và góc để cm 2 tam giác đồng dạng.
Ví dụ:
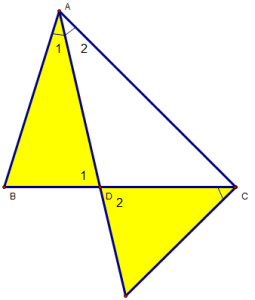
Cho tam giác ABC có AB a) Chứng minh rằng ∆ADB đồng dạng ∆CDI.
b) Chứng minh rằng AD/AC = AB/AI.
c) Chứng minh rằng AD² = AB.AC – BD.DC.
Alt: Sơ đồ chứng minh tam giác ADB và tam giác CDI đồng dạng, sử dụng yếu tố góc và đường phân giác AD.
Hướng dẫn giải:
a) Xét hai tam giác ∆ADB và ∆CDI, ta có:
- Góc BCx = góc BAD (giả thiết).
- Góc D1 = góc D2 (đối đỉnh).
=> ∆ADB ~ ∆CDI (g-g).
b) Xét hai tam giác ∆ABD và ∆AIC, ta có:
- Góc B = góc I (do ∆ADB ~ ∆CDI).
- Góc A1 = góc A2 (AD là phân giác).
=> ∆ABD ~ ∆AIC (g-g) => AD/AC = AB/AI.
c) Từ kết quả câu b, ta có: AD.AI = AB.AC (1).
Từ ∆ADB ~ ∆CDI, ta có: AD/CD = BD/DI => AD.DI = BD.CD (2).
Lấy (1) – (2): AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI) = AD.AD = AD².
Vậy AD² = AB.AC – BD.CD.
Dạng 2: Sử Dụng Định Lý Talet và Tính Chất Đường Thẳng Song Song
Dạng bài này thường liên quan đến việc cm 2 tam giác đồng dạng thông qua định lý Talet và các tính chất của đường thẳng song song.
Ví dụ:
Cho tam giác ABC nhọn. Vẽ hai đường cao BD và CE. Vẽ DF và EG lần lượt là đường cao của tam giác ADE.
a) Chứng minh rằng ∆ABD ~ ∆AEG.
b) Chứng minh rằng AD.AE = AB.AG = AC.AF.
c) Chứng minh rằng FG // BC.
Alt: Hình vẽ minh họa hai tam giác ABD và AEG, với các đường cao BD, CE, DF và EG, áp dụng định lý Talet.
Hướng dẫn giải:
a) Xét ∆ABD và ∆AEG, ta có:
- BD ⊥ AC (BD là đường cao).
- EG ⊥ AC (EG là đường cao).
=> BD // EG => ∆ABD ~ ∆AGE (g-g).
b) Từ ∆ABD ~ ∆AGE, ta có: AB/AE = AD/AG => AD.AE = AB.AG (1).
Chứng minh tương tự, ta được: AD.AE = AC.AF (2).
Từ (1) và (2) => AD.AE = AB.AG = AC.AF.
c) Xét ∆ABC, ta có: AB/AF = AC/AG => FG // BC (định lý Talet đảo).
Dạng 3: Sử Dụng Góc Tương Ứng Bằng Nhau
Trong dạng bài này, việc tìm ra các góc tương ứng bằng nhau là chìa khóa để cm 2 tam giác đồng dạng.
Ví dụ:
Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng ∆HBE đồng dạng ∆HCD.
b) Chứng minh rằng ∆HED đồng dạng ∆HBC và góc HDE = góc HAE.
c) Biết rằng BD = CE. Gọi M là giao điểm của AH và BC. Chứng minh rằng: DE vuông góc EM.
Alt: Hình vẽ hai tam giác HBE và tam giác HCD, minh họa việc chứng minh đồng dạng qua các góc đối đỉnh và góc vuông.
Hướng dẫn giải:
a) Xét hai tam giác ∆HBE và ∆HCD, ta có:
- Góc BEH = góc CDH = 90° (giả thiết).
- Góc EHB = góc DHC (đối đỉnh).
=> ∆HBE ~ ∆HCD (g-g).
b) Từ ∆HBE ~ ∆HCD => HE/HD = HB/HC => HE/HB = HD/HC.
Xét ∆HED và ∆HBC, ta có:
- HE/HB = HD/HC.
- Góc EHD = góc CHB (đối đỉnh).
=> ∆HED ~ ∆HBC (c-g-c) => Góc HDE = góc HAE.
c) Vì BD = CE và ∆HBE ~ ∆HCD => HB = HC => ∆HBC cân tại H.
Chứng minh tương tự câu b, ta có ∆HED ~ ∆HBC. Vì ∆HBC cân tại H, nên ∆HED cũng cân tại H => HE = HD.
Gọi giao điểm của DE và AH là I. Khi đó, HI là đường cao đồng thời là đường trung tuyến của ∆HED => DI = IE.
Xét ∆DEM, có DI = IE và BM = MC (vì H là trực tâm và BD = CE) => MI là đường trung bình của ∆DEC => MI // EC => MI ⊥ DE. Vậy DE ⊥ EM.
Lời Kết
Việc cm 2 tam giác đồng dạng đòi hỏi sự hiểu biết vững chắc về lý thuyết, kỹ năng quan sát và phân tích hình vẽ, cũng như khả năng vận dụng linh hoạt các phương pháp chứng minh. Hy vọng rằng, với những kiến thức và ví dụ minh họa chi tiết trong bài viết này, các em học sinh sẽ tự tin hơn trong việc chinh phục các bài toán hình học liên quan đến tam giác đồng dạng và đạt được kết quả cao trong học tập.