Chuyển động thẳng biến đổi đều là một dạng chuyển động cơ bản và quan trọng trong chương trình Vật lý THPT. Để hiểu rõ bản chất và các công thức liên quan, chúng ta sẽ đi sâu vào định nghĩa, phân loại, các phương trình và đồ thị đặc trưng của chuyển động này.
1. Vận tốc tức thời và chuyển động biến đổi đều
1.1. Khái niệm về vận tốc tức thời
Vận tốc tức thời cho biết độ nhanh, chậm của vật tại một thời điểm nhất định. Nó được tính bằng tỉ số giữa độ dời rất nhỏ và khoảng thời gian rất ngắn.
$v=frac{Delta s}{Delta t}$
1.2. Véctơ vận tốc
Véctơ vận tốc đặc trưng cho cả độ lớn và hướng của chuyển động, với gốc đặt tại vật, phương và chiều trùng với phương và chiều của chuyển động, độ dài biểu thị độ lớn của vận tốc.
2. Chuyển Động Thẳng Biến Đổi Đều
2.1. Định nghĩa
Chuyển động Thẳng Biến đổi đều Là Chuyển động mà trong đó gia tốc tức thời không đổi. Quỹ đạo của chuyển động là đường thẳng, và độ lớn của vận tốc tức thời tăng hoặc giảm đều theo thời gian. Đây là một dạng chuyển động có gia tốc đặc biệt, đóng vai trò quan trọng trong việc mô tả nhiều hiện tượng vật lý thực tế.
Hình ảnh minh họa định nghĩa chuyển động thẳng biến đổi đều, thể hiện gia tốc a không đổi theo thời gian.
2.2. Các loại chuyển động thẳng biến đổi đều
Có hai loại chính của chuyển động thẳng biến đổi đều, phân biệt dựa trên sự thay đổi của vận tốc:
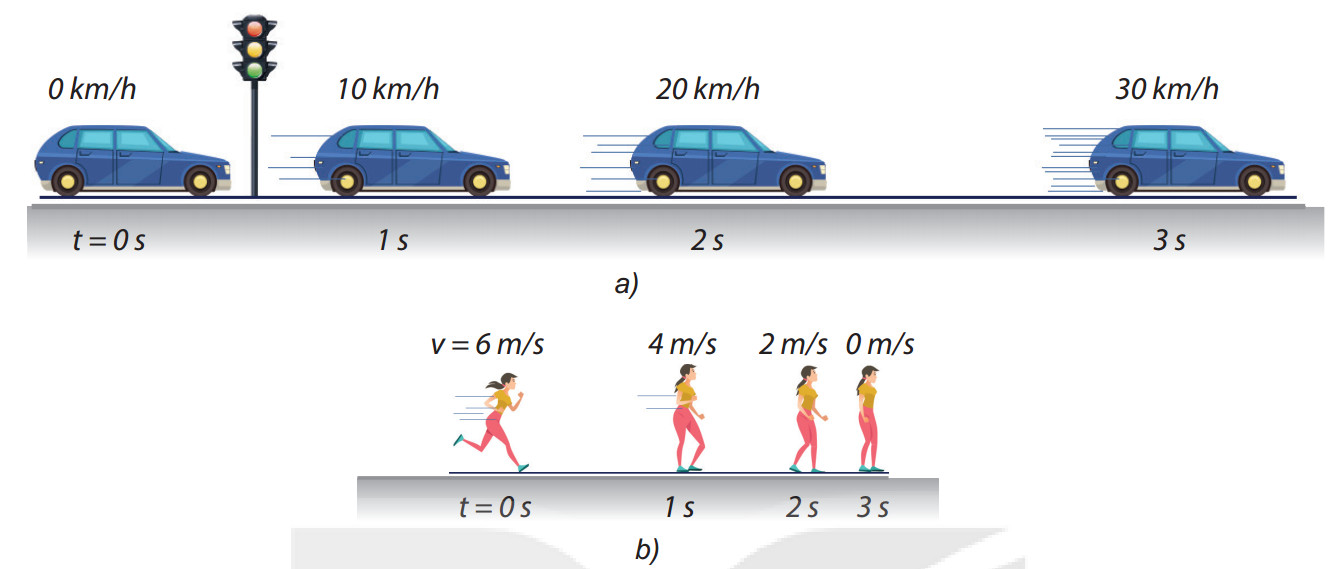
2.2.1. Chuyển động nhanh dần đều
Khi độ lớn của vận tốc tức thời tăng đều theo thời gian, ta có chuyển động nhanh dần đều. Trong trường hợp này, gia tốc và vận tốc cùng dấu.
2.2.2. Chuyển động chậm dần đều
Ngược lại, khi độ lớn của vận tốc tức thời giảm đều theo thời gian, ta có chuyển động chậm dần đều. Lúc này, gia tốc và vận tốc trái dấu.
Hình ảnh so sánh chuyển động nhanh dần đều (gia tốc và vận tốc cùng hướng) và chậm dần đều (gia tốc và vận tốc ngược hướng).
2.3. Các phương trình của chuyển động thẳng biến đổi đều
Các phương trình sau đây mô tả mối quan hệ giữa các đại lượng trong chuyển động thẳng biến đổi đều:
2.3.1. Phương trình gia tốc
$vec{a}=frac{vec{v}-vec{v_o}}{Delta t}$ có độ lớn $a=frac{v-v_o}{Delta t}$
2.3.2. Phương trình toạ độ – thời gian
$x=x_o+v_ot+frac{1}{2}at^2$
Trong đó:
$x_0$ : Tọa độ ban đầu
$v_0$: Vận tốc ban đầu
t: Thời gian chuyển động
2.3.3. Phương trình vận tốc
$v=v_0+at$
Trong đó:
$v_0$: Vận tốc ban đầu
a: Gia tốc
t: Thời gian chuyển động
2.3.4. Hệ thức độc lập thời gian
$v^2-v_0^2=2a Delta x (x=x-x_0)$
2.4. Đồ thị của chuyển động thẳng biến đổi đều
Các đồ thị sau đây giúp ta hình dung và phân tích chuyển động thẳng biến đổi đều:
2.4.1. Đồ thị tọa độ theo thời gian (x-t)
Đồ thị có dạng một nhánh parabol. Độ cong của parabol phụ thuộc vào gia tốc.
Hình ảnh minh họa đồ thị tọa độ theo thời gian (x-t) của chuyển động thẳng biến đổi đều, có dạng parabol.
2.4.2. Đồ thị vận tốc theo thời gian (v-t)
Đồ thị là một đường thẳng xiên góc. Hệ số góc của đường thẳng này chính là gia tốc của chuyển động.
Hình ảnh minh họa đồ thị vận tốc theo thời gian (v-t) của chuyển động thẳng biến đổi đều, có dạng đường thẳng.
Hệ số góc của đường biểu diễn vận tốc theo thời gian (v – t) bằng gia tốc của chuyển động:
$a=tan Alpha =frac{v-v_o}{t}$
2.4.3. Đồ thị gia tốc theo thời gian (a-t)
Đồ thị là một đường thẳng song song với trục thời gian, biểu thị gia tốc không đổi.
Hình ảnh minh họa đồ thị gia tốc theo thời gian (a-t) của chuyển động thẳng biến đổi đều, có dạng đường thẳng song song với trục thời gian.
3. Ứng dụng và bài tập
Chuyển động thẳng biến đổi đều là chuyển động thường gặp trong thực tế, ví dụ như chuyển động của ô tô khi tăng tốc hoặc phanh, chuyển động của vật rơi tự do (trong điều kiện gần đúng). Việc nắm vững kiến thức về chuyển động này giúp giải quyết nhiều bài toán vật lý và hiểu rõ các hiện tượng tự nhiên.
(Phần bài tập và sơ đồ tư duy từ bài gốc có thể được sử dụng ở đây)