Trong chương trình hình học lớp 9, việc Chứng Minh Tam Giác Nội Tiếp đường Tròn là một kỹ năng quan trọng. Nó không chỉ giúp học sinh nắm vững kiến thức về đường tròn mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề. Bài viết này sẽ cung cấp một cái nhìn tổng quan về lý thuyết và các dạng bài tập thường gặp liên quan đến việc chứng minh một tam giác nội tiếp đường tròn.
I. Lý thuyết cơ bản về tam giác nội tiếp
1. Định nghĩa tam giác nội tiếp
Một tam giác được gọi là tam giác nội tiếp đường tròn nếu cả ba đỉnh của tam giác đó đều nằm trên đường tròn. Ngược lại, đường tròn đó được gọi là đường tròn ngoại tiếp tam giác.
Ví dụ minh họa:
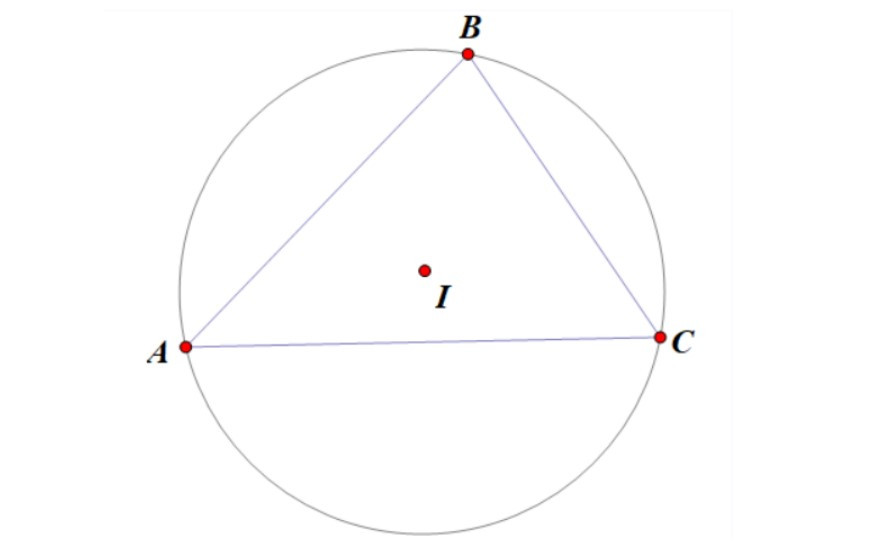
Trong hình trên, tam giác ABC có ba đỉnh A, B, C nằm trên đường tròn tâm I. Do đó, tam giác ABC là một tam giác nội tiếp đường tròn tâm I. Đường tròn tâm I là đường tròn ngoại tiếp tam giác ABC.
2. Định lý quan trọng
Mọi tam giác đều có một và chỉ một đường tròn ngoại tiếp. Điều này có nghĩa là, với bất kỳ tam giác nào, ta luôn có thể vẽ được một đường tròn đi qua cả ba đỉnh của nó.
3. Cách xác định tâm đường tròn ngoại tiếp
Tâm của đường tròn ngoại tiếp một tam giác có thể được xác định bằng một trong các cách sau:
- Giao điểm của ba đường trung trực: Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực của ba cạnh của tam giác.
- Tam giác vuông: Trong một tam giác vuông, trung điểm của cạnh huyền chính là tâm của đường tròn ngoại tiếp tam giác đó.
- Tam giác đều: Trong một tam giác đều, tâm của đường tròn ngoại tiếp trùng với tâm của đường tròn nội tiếp.
II. Các phương pháp chứng minh tam giác nội tiếp đường tròn
Để chứng minh tam giác nội tiếp đường tròn, chúng ta thường sử dụng các phương pháp sau:
- Chứng minh ba điểm cách đều một điểm: Nếu chứng minh được ba đỉnh của tam giác cách đều một điểm, thì điểm đó chính là tâm của đường tròn ngoại tiếp tam giác, và tam giác đó nội tiếp đường tròn.
- Sử dụng tính chất góc nội tiếp: Nếu một góc nội tiếp chắn nửa đường tròn thì góc đó là góc vuông. Ngược lại, nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
- Sử dụng định lý đảo về tứ giác nội tiếp: Chứng minh một tứ giác có bốn đỉnh cùng nằm trên một đường tròn, sau đó suy ra tam giác tạo bởi ba trong bốn đỉnh đó nội tiếp đường tròn.
- Chứng minh tổng hai góc đối bằng 180 độ: Nếu có một tứ giác mà tổng hai góc đối của nó bằng 180 độ, thì tứ giác đó nội tiếp được trong một đường tròn. Từ đó suy ra các tam giác liên quan cũng nội tiếp đường tròn.
III. Bài tập vận dụng chứng minh tam giác nội tiếp
Bài tập 1: Chứng minh tam giác có tâm đường tròn ngoại tiếp là trung điểm cạnh huyền là tam giác vuông.
Cho tam giác ABC, O là trung điểm cạnh BC và OA = OB = OC. Chứng minh tam giác ABC vuông tại A.
Hướng dẫn giải:
Vì OA = OB = OC nên O là tâm đường tròn ngoại tiếp tam giác ABC. Do đó, tam giác ABC nội tiếp đường tròn đường kính BC. Theo tính chất của tam giác nội tiếp đường tròn, tam giác ABC vuông tại A.
Bài tập 2: Chứng minh nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Cho tam giác ABC nội tiếp đường tròn tâm O, cạnh BC là đường kính. Chứng minh tam giác ABC vuông tại A.
Hướng dẫn giải:
Vì BC là đường kính của đường tròn tâm O, nên góc BAC là góc nội tiếp chắn nửa đường tròn. Do đó, góc BAC = 90 độ. Suy ra tam giác ABC vuông tại A. (Dựa theo tính chất đường trung tuyến trong tam giác vuông).
Bài tập 3: Bài tập trắc nghiệm:
Chọn đáp án đúng: Tâm của đường tròn ngoại tiếp tam giác nhọn nằm ở đâu?
A. Bên ngoài tam giác
B. Bên trong tam giác
C. Trên cạnh của tam giác
D. Trùng với trọng tâm tam giác
Đáp án: B. Bên trong tam giác.
IV. Lời khuyên khi giải bài tập chứng minh tam giác nội tiếp
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, định lý và tính chất liên quan đến đường tròn và tam giác.
- Vẽ hình chính xác: Một hình vẽ rõ ràng và chính xác sẽ giúp bạn dễ dàng nhận ra các mối quan hệ hình học.
- Phân tích đề bài: Đọc kỹ đề bài, xác định rõ giả thiết và kết luận cần chứng minh.
- Lựa chọn phương pháp phù hợp: Dựa vào giả thiết và kết luận, chọn phương pháp chứng minh thích hợp.
- Trình bày rõ ràng: Viết các bước chứng minh một cách logic và dễ hiểu.
Việc chứng minh tam giác nội tiếp đường tròn đòi hỏi sự kết hợp giữa kiến thức lý thuyết và kỹ năng giải bài tập. Hy vọng bài viết này sẽ giúp các bạn học sinh nắm vững kiến thức và tự tin hơn khi giải các bài tập liên quan.