Định lý Menelaus là một công cụ mạnh mẽ trong hình học phẳng, cho phép chứng minh các điểm thẳng hàng. Cùng với định lý Ceva, nó tạo thành bộ đôi hữu ích để giải quyết nhiều bài toán hình học phức tạp. Bài viết này sẽ đi sâu vào định lý Menelaus, cách chứng minh và mở rộng nó cho đa giác bất kỳ.
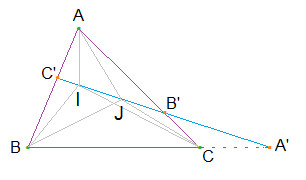
Định lý Menelaus: Cho tam giác $ABC$ và ba điểm $A’$, $B’$, $C’$ lần lượt nằm trên ba đường thẳng $BC$, $CA$, $AB$. Ba điểm $A’$, $B’$, $C’$ thẳng hàng khi và chỉ khi:
$$frac{vec{A’B}}{vec{A’C}} times frac{vec{B’C}}{vec{B’A}} times frac{vec{C’A}}{vec{C’B}} = 1.$$
Để hiểu rõ định lý Menelaus, chúng ta cần làm quen với khái niệm tỷ lệ có dấu.
Tỷ Lệ Có Dấu
Tỷ lệ có dấu là một khái niệm quan trọng để hiểu và áp dụng định lý Menelaus một cách chính xác.
Ký hiệu $frac{vec{A’B}}{vec{A’C}}$ biểu thị tỷ lệ có dấu. Khác với tỷ lệ thông thường luôn dương, tỷ lệ có dấu có thể âm hoặc dương, tùy thuộc vào hướng của các vectơ.
Ví dụ, xét hình vẽ dưới đây:
Trong hình này, tỷ lệ thông thường $frac{UX}{UY} = 2$, nhưng tỷ lệ có dấu $frac{vec{UX}}{vec{UY}} = -2$ vì $vec{UX}$ và $vec{UY}$ ngược hướng nhau. Tỷ lệ có dấu là dương nếu hai vectơ cùng hướng và âm nếu ngược hướng.
Tại sao cần tỷ lệ có dấu?
Tỷ lệ thông thường không thể xác định duy nhất một điểm trên đường thẳng. Tỷ lệ có dấu khắc phục nhược điểm này.
Ví dụ, trên đường thẳng $XY$, cần tìm điểm $Z$ sao cho $frac{ZX}{ZY} = 2$.
Có hai điểm $U$ và $V$ thỏa mãn $frac{UX}{UY} = frac{VX}{VY} = 2$ nếu dùng tỷ lệ thông thường. Nhưng chỉ có duy nhất điểm $V$ thỏa mãn $frac{vec{VX}}{vec{VY}} = 2$ nếu dùng tỷ lệ có dấu.
Điểm $U$ không thỏa mãn vì $frac{vec{UX}}{vec{UY}} = -2 neq 2$.
Chứng Minh Định Lý Menelaus
Để chứng minh định lý Menelaus, chúng ta sử dụng định lý về tỷ lệ diện tích.
Định lý về tỷ lệ diện tích: Cho hai tam giác $ABU$ và $ABV$ có chung cạnh $AB$. Đường thẳng nối $UV$ cắt $AB$ tại $T$. Khi đó:
$$frac{overline{s}(ABU)}{overline{s}(ABV)} = frac{vec{TU}}{vec{TV}}.$$
Trong đó $overline{s}$ kí hiệu diện tích có dấu của tam giác.
Chứng minh định lý Menelaus:
Giả sử $A’$, $B’$, $C’$ thẳng hàng. Lấy hai điểm bất kỳ $I$ và $J$ trên đường thẳng $A’B’C’$. Theo định lý về tỷ lệ diện tích, ta có:
$$frac{vec{A’B}}{vec{A’C}} = frac{overline{s}(IJB)}{overline{s}(IJC)}, ~~frac{vec{B’C}}{vec{B’A}} = frac{overline{s}(IJC)}{overline{s}(IJA)}, ~~frac{vec{C’A}}{vec{C’B}} = frac{overline{s}(IJA)}{overline{s}(IJB)}.$$
Nhân các tỷ lệ này lại, ta được:
$$frac{vec{A’B}}{vec{A’C}} times frac{vec{B’C}}{vec{B’A}} times frac{vec{C’A}}{vec{C’B}} = frac{overline{s}(IJB)}{overline{s}(IJC)} times frac{overline{s}(IJC)}{overline{s}(IJA)} times frac{overline{s}(IJA)}{overline{s}(IJB)} = 1.$$
Trường hợp ngược lại được chứng minh tương tự như định lý Ceva.
Mở Rộng Định Lý Menelaus Cho Đa Giác
Định lý Menelaus không chỉ giới hạn cho tam giác mà còn có thể mở rộng cho đa giác bất kỳ.
Định lý Menelaus cho ngũ giác: Cho ngũ giác $A_1 A_2 A_3 A_4 A_5$ và năm điểm $B_1$, $B_2$, $B_3$, $B_4$, $B_5$ lần lượt nằm trên năm đường thẳng $A_1 A_2$, $A_2 A_3$, $A_3 A_4$, $A_4 A_5$, $A_5 A_1$. Nếu các điểm $B_1$, $B_2$, $B_3$, $B_4$, $B_5$ thẳng hàng thì:
$$frac{vec{B_1 A_1}}{vec{B_1 A_2}} times frac{vec{B_2 A_2}}{vec{B_2 A_3}} times frac{vec{B_3 A_3}}{vec{B_3 A_4}} times frac{vec{B_4 A_4}}{vec{B_4 A_5}} times frac{vec{B_5 A_5}}{vec{B_5 A_1}}= 1.$$
Chứng minh tương tự như trường hợp tam giác.
Tổng quát, định lý Menelaus cho đa giác: Cho đa giác $n$-cạnh $A_1 A_2 dots A_n$ và $n$ điểm $B_1$, …, $B_n$, trong đó điểm $B_i$ nằm trên đường thẳng $A_i A_{i+1}$. Nếu các điểm $B_1$, $B_2$, …, $B_n$ thẳng hàng thì:
$$prod_{i=1}^{n} frac{vec{B_i A_i}}{vec{B_i A_{i+1}}} = 1.$$
Kết Luận
Định lý Menelaus là một công cụ mạnh mẽ để chứng minh tính thẳng hàng trong hình học. Việc hiểu rõ khái niệm tỷ lệ có dấu và định lý về tỷ lệ diện tích giúp việc chứng minh trở nên đơn giản và dễ dàng mở rộng cho đa giác. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn sâu sắc về định lý Menelaus và ứng dụng của nó.