Góc giữa đường thẳng và mặt phẳng là một khái niệm quan trọng trong chương trình hình học không gian lớp 11. Việc nắm vững kiến thức và phương pháp giải các dạng bài tập liên quan đến góc giữa đường thẳng và mặt phẳng sẽ giúp học sinh tự tin hơn khi đối diện với các bài toán hình học. Bài viết này sẽ cung cấp đầy đủ lý thuyết, phương pháp chứng minh và các bài tập minh họa từ cơ bản đến nâng cao để các em học sinh có thể dễ dàng chinh phục dạng toán này.
1. Lý Thuyết Về Góc Giữa Đường Thẳng và Mặt Phẳng
1.1. Định Nghĩa Góc Giữa Đường Thẳng và Mặt Phẳng
- Nếu đường thẳng vuông góc với mặt phẳng (P) thì góc giữa đường thẳng đó và mặt phẳng (P) bằng 90°.
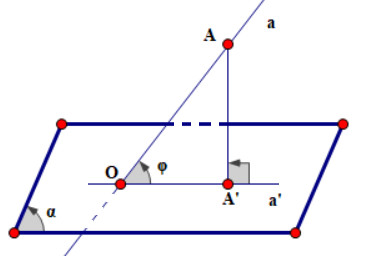
- Nếu đường thẳng không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng đó và hình chiếu của nó trên (P) được gọi là góc giữa đường thẳng và mặt phẳng (P).
Hình ảnh minh họa cách xác định góc giữa đường thẳng và mặt phẳng trong không gian.
1.2. Ký Hiệu Góc Giữa Đường Thẳng và Mặt Phẳng
Nếu đường thẳng α vuông góc với (P) thì góc giữa α và (P) ký hiệu là .
Nếu đường thẳng α không vuông góc với (P) thì góc giữa α và (P) là góc giữa α và α’, với α’ là hình chiếu của α trên (P).
Lưu ý: .
2. Hướng Dẫn Cách Xác Định Góc Giữa Đường Thẳng và Mặt Phẳng
2.1. Tính Góc Giữa Đường Thẳng và Mặt Phẳng Bằng Phương Pháp Vectơ
- Gọi vectơ u = (a;b) là vectơ chỉ phương của đường thẳng a.
- Gọi n = (A;B) là vectơ pháp tuyến của mặt phẳng (P).
Khi đó, góc α giữa đường thẳng a và mặt phẳng (P) được tính theo công thức:
Ví dụ: Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau đôi một. Khẳng định nào sau đây đúng?
A. Góc giữa AC và (BCD) là góc ACB
B. Góc giữa AD và (ABC) là góc ADB
C. Góc giữa AC và (ABD) là góc CAB
D. Góc giữa CD và (ABD) là góc CBD
Giải:
Hình ảnh minh họa ví dụ về tính góc giữa đường thẳng và mặt phẳng bằng phương pháp vectơ trong hình học không gian.
Từ giả thiết ta có:
⇒ (AC,(BCD))= ACB
⇒ Chọn đáp án: A
2.2. Cách Xác Định Góc Giữa Đường Thẳng và Mặt Phẳng Bằng Phương Pháp Hình Học
- Tìm giao điểm I của đường thẳng d và mặt phẳng (P): I = .
- Tìm điểm A thuộc d, kẻ AH vuông góc với (P).
- Góc giữa d và (P) là góc .
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo góc giữa SA và (ABC).
A. 60°
B. 90°
C. 45°
D. 30°
Hình ảnh minh họa ví dụ về cách xác định góc giữa đường thẳng và mặt phẳng bằng phương pháp hình học.
Lời giải:
Do H là hình chiếu của S lên mặt phẳng (ABC) nên SH$perp$ (ABC)
Vậy AH là hình chiếu của SA lên mp(ABC)
(SA, (ABC)) = (SA, AH) =
Ta có: =>
Mà: ⩟ ABC = ⩟ SBC => SH=AH
Vậy tam giác SAH vuông cân tại H =>
=> Chọn C
3. Bài Tập Trắc Nghiệm Minh Họa Góc Giữa Đường Thẳng và Mặt Phẳng Từ Cơ Bản Đến Nâng Cao
Câu 1. Cho hình thoi ABCD có tâm O, AC = 2a; BD = 2AC. Lấy điểm S không thuộc (ABCD) sao cho SO (ABCD). Biết tan (SBO) = ½. Tính số đo của góc giữa SC và (ABCD):
A. 30°
B. 45°
C. 60°
D. 90°
Câu 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC):
A. 30°
B. 45°
C. 60°
D. 75°
Câu 3. Cho hình chóp S.ABC có SAperp (ABC) và tam giác ABC không vuông. Gọi H, K lần lượt là trực tâm tam giác ABC và tam giác SBC. Số đo góc tạo bởi SC và (BHK) là:
A. 45°
B. 120°
C. 90°
D. 65°
Câu 4. Cho hình chóp S. ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với mp (ABCD). Gọi α là góc giữa BD và mp (SAD). Chọn khẳng định đúng trong các khẳng định sau?
A.
B.
C.
D.
Câu 5. Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, (ABCD), SA = . Gọi là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
A.
B.
C.
D.
Câu 6. Cho hình lập phương ABCD. A’B’C’D’ cạnh a. Gọi là góc giữa AC và mp ( A’BCD’). Chọn khẳng định đúng trong các khẳng định sau?
A.
B.
C.
D.
Câu 7. Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, SA = 2a và SA vuông góc với mặt phẳng đáy (ABCD), góc giữa cạnh SC và mặt phẳng (ABCD) là?
A.
B.
C.
D.
Câu 8. Cho hình chóp SABCD đáy ABCD là hình chữ nhật, AB=a, AD=2a, cạnh bên SA vuông góc với đáy. Góc giữa SC và đáy ABCD bằng 60°. Tính độ dài SA?
A. SA =
B. SA =
C. SA =
D. SA =
Câu 9. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A, B biết AB=BC=a, AD=2a, SA vuông góc với mặt phẳng đáy (ABCD). Tính độ dài SA để góc giữa SC và mặt phẳng (ABCD) bằng 45°.
A. SA =
B. SA =
C. SA =
D. SA =
Câu 10. Cho hình chóp SABC có SA = a, SA vuông góc với đáy, ABC là tam giác vuông cân tại B, góc , AC = 2a. Tính góc giữa SC và mặt phẳng (SAB).
A.
B.
C.
D.
Hy vọng bài viết này đã cung cấp đầy đủ kiến thức và phương pháp giải các bài toán liên quan đến góc giữa đường thẳng và mặt phẳng. Chúc các em học tốt!