Trong hình học, một trong những tính chất quan trọng và thú vị của tam giác vuông liên quan đến đường trung tuyến ứng với cạnh huyền. Tính chất này không chỉ giúp giải quyết các bài toán hình học một cách dễ dàng hơn mà còn là nền tảng để hiểu sâu hơn về cấu trúc của tam giác vuông. Bài viết này sẽ trình bày chi tiết về cách Chứng Minh đường Trung Tuyến Trong Tam Giác Vuông, cùng với các ứng dụng của nó.
Định lý:
- Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
- Ngược lại, nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó, thì tam giác đó là tam giác vuông.
Bài toán:
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng:
- Nếu góc A = 90° thì MA = ½ BC
- Nếu MA = ½ BC thì góc A = 90°
Chứng minh:
Để chứng minh định lý này, chúng ta sẽ sử dụng phương pháp dựng thêm hình phụ và các kiến thức về tam giác bằng nhau, song song và các góc tạo bởi đường thẳng song song.
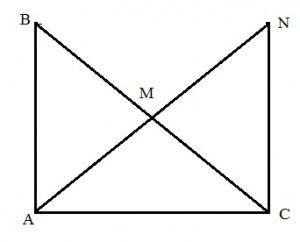Hình vẽ minh họa chứng minh đường trung tuyến trong tam giác vuông
Alt: Hình vẽ tam giác ABC vuông tại A, M là trung điểm BC, N đối xứng với A qua M để chứng minh AM = 1/2 BC
Chứng minh phần 1: Nếu góc A = 90° thì MA = ½ BC
Xét tam giác ABC có M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm N sao cho MN = MA.
Ta có:
- góc AMB = góc NMC (đối đỉnh)
- BM = CM (M là trung điểm BC)
- MA = MN (theo cách dựng)
Suy ra: tam giác MAB = tam giác MNC (c.g.c)
Từ đó suy ra:
- NC = AB
- góc MBA = góc MCN
Do góc MBA = góc MCN nên AB // NC, suy ra góc BAC + góc ACN = 180°.
Vì góc BAC = 90° (giả thiết) nên góc ACN = 90°.
Khi đó, tam giác ABC = tam giác CNA (c.g.c) vì:
- AC chung
- AB = NC (chứng minh trên)
- góc BAC = góc ACN = 90°
Do đó: AN = BC => AM = ½ BC (vì AM = 1/2 AN)
Chứng minh phần 2: Nếu MA = ½ BC thì góc A = 90°
Ta có: MA = ½ AN. Nếu MA = ½ BC thì AN = BC.
Lại có AB = CN (chứng minh trên)
Suy ra tam giác ABC = tam giác CNA (c.c.c), suy ra: góc BAC = góc ACN.
Mà góc BAC + góc ACN = 180° (vì AB // CA) nên góc BAC = 90° (điều phải chứng minh).
Kết luận:
Chứng minh trên đã làm sáng tỏ tính chất quan trọng của đường trung tuyến trong tam giác vuông. Việc hiểu rõ và vận dụng linh hoạt định lý này sẽ giúp các em học sinh giải quyết các bài toán hình học liên quan một cách hiệu quả và chính xác. Đây cũng là một kiến thức nền tảng quan trọng trong chương trình hình học THCS.