Đường cao là một khái niệm quan trọng trong hình học, đặc biệt là khi nghiên cứu về tam giác. Hiểu rõ về đường cao và cách chứng minh chúng sẽ giúp bạn giải quyết nhiều bài toán hình học một cách dễ dàng và hiệu quả hơn.
1. Định Nghĩa và Tính Chất Cơ Bản của Đường Cao
Đường cao của một tam giác là đoạn thẳng vuông góc kẻ từ một đỉnh của tam giác đến đường thẳng chứa cạnh đối diện. Mỗi tam giác có ba đường cao, và ba đường cao này có một số tính chất quan trọng.
1.1. Ba Đường Cao Đồng Quy
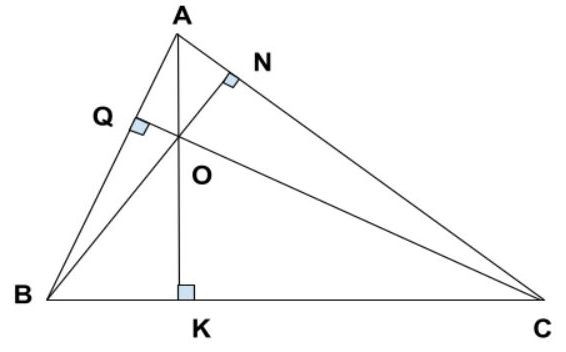
Một trong những tính chất quan trọng nhất của đường cao là ba đường cao của một tam giác (hoặc đường kéo dài của chúng) luôn đồng quy tại một điểm. Điểm đồng quy này được gọi là trực tâm của tam giác.
Cách chứng minh ba đường cao đồng quy:
Có nhiều cách để chứng minh tính chất này, một trong số đó là sử dụng định lý Ceva.
- Định lý Ceva: Cho tam giác ABC, các điểm D, E, F lần lượt nằm trên các cạnh BC, CA, AB. Khi đó, AD, BE, CF đồng quy khi và chỉ khi (BD/DC) (CE/EA) (AF/FB) = 1.
Để chứng minh ba đường cao đồng quy, ta cần chứng minh rằng tích trên bằng 1 khi AD, BE, CF là các đường cao. Điều này có thể được thực hiện bằng cách sử dụng các tính chất của tam giác vuông và các tỷ lệ đoạn thẳng.
1.2. Đường Cao và Diện Tích Tam Giác
Đường cao đóng vai trò quan trọng trong việc tính diện tích tam giác. Diện tích tam giác có thể được tính bằng công thức:
Diện tích = (1/2) cạnh đáy chiều cao tương ứng
2. Đường Cao trong Các Loại Tam Giác Đặc Biệt
Đường cao có những tính chất đặc biệt trong các loại tam giác như tam giác vuông, tam giác cân và tam giác đều.
2.1. Đường Cao trong Tam Giác Vuông
Trong một tam giác vuông, hai cạnh góc vuông chính là hai đường cao của tam giác đó. Đường cao thứ ba, kẻ từ đỉnh góc vuông xuống cạnh huyền, có những tính chất quan trọng liên quan đến các cạnh của tam giác.
- Hệ thức lượng trong tam giác vuông:
- h² = b’ * c’ (bình phương đường cao bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền)
- a h = b c (tích của cạnh huyền và đường cao bằng tích của hai cạnh góc vuông)
2.2. Đường Cao trong Tam Giác Cân
Trong một tam giác cân, đường cao kẻ từ đỉnh cân đồng thời là đường trung tuyến, đường phân giác và đường trung trực của cạnh đáy.
Cách Chứng Minh đường Cao là đường trung tuyến trong tam giác cân:
Xét tam giác ABC cân tại A, đường cao AH. Ta cần chứng minh H là trung điểm của BC.
- Vì tam giác ABC cân tại A, nên AB = AC.
- Vì AH là đường cao, nên góc AHB = góc AHC = 90 độ.
- AH là cạnh chung.
- Vậy tam giác AHB bằng tam giác AHC (cạnh huyền – cạnh góc vuông).
- Suy ra HB = HC (hai cạnh tương ứng).
- Vậy H là trung điểm của BC, suy ra AH là đường trung tuyến.
2.3. Đường Cao trong Tam Giác Đều
Trong một tam giác đều, ba đường cao có độ dài bằng nhau và đồng thời là đường trung tuyến, đường phân giác và đường trung trực của các cạnh.
Công thức tính đường cao trong tam giác đều:
Nếu cạnh của tam giác đều là a, thì đường cao h = (a√3)/2
3. Ứng Dụng của Đường Cao trong Giải Toán
Đường cao là một công cụ mạnh mẽ để giải quyết nhiều bài toán hình học. Dưới đây là một số ví dụ:
- Tính diện tích tam giác: Khi biết độ dài một cạnh và đường cao tương ứng, ta có thể dễ dàng tính được diện tích tam giác.
- Chứng minh các đường thẳng đồng quy: Sử dụng định lý Ceva hoặc các tính chất của trực tâm để chứng minh các đường thẳng đồng quy.
- Giải các bài toán liên quan đến hệ thức lượng trong tam giác vuông: Áp dụng các hệ thức lượng để tìm độ dài các cạnh hoặc đường cao trong tam giác vuông.
- Xác định các yếu tố của tam giác cân và tam giác đều: Sử dụng các tính chất của đường cao trong tam giác cân và tam giác đều để tìm các yếu tố còn thiếu của tam giác.
4. Các Phương Pháp Chứng Minh Đường Cao
Để chứng minh một đoạn thẳng là đường cao của tam giác, ta cần chứng minh nó vuông góc với cạnh đối diện. Dưới đây là một số phương pháp thường được sử dụng:
- Sử dụng định nghĩa: Chứng minh đoạn thẳng đó vuông góc với cạnh đối diện bằng cách sử dụng các tính chất của góc vuông hoặc các đường thẳng vuông góc.
- Sử dụng định lý Pythagoras: Nếu biết độ dài các cạnh của tam giác, ta có thể sử dụng định lý Pythagoras để chứng minh tam giác đó vuông tại một đỉnh, và do đó đường cao kẻ từ đỉnh đó vuông góc với cạnh đối diện.
- Sử dụng các tính chất của tam giác đặc biệt: Trong tam giác cân hoặc tam giác đều, ta có thể sử dụng các tính chất đặc biệt của đường cao để chứng minh.
- Sử dụng các định lý về đồng dạng: Chứng minh hai tam giác đồng dạng và sử dụng các tỷ lệ cạnh tương ứng để suy ra tính vuông góc.
Hiểu rõ về đường cao và các phương pháp chứng minh chúng sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán hình học, đồng thời phát triển tư duy logic và khả năng sáng tạo trong học tập.