1. Khái niệm hình chóp tam giác đều
Hình Chóp Tam Giác đều là một hình không gian đặc biệt với những tính chất hình học thú vị. Để hiểu rõ về nó, chúng ta cần nắm vững định nghĩa và các yếu tố cấu thành.
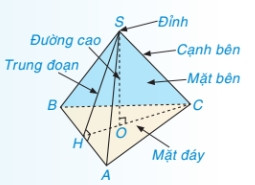
- Định nghĩa: Hình chóp tam giác đều là hình chóp có đáy là một tam giác đều và các mặt bên là các tam giác cân bằng nhau, có chung một đỉnh. Đỉnh chung này được gọi là đỉnh của hình chóp tam giác đều.
- Đường cao: Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy được gọi là đường cao của hình chóp tam giác đều. Đường cao này vuông góc với mặt phẳng đáy tại trọng tâm của tam giác đều.
- Trung đoạn: Đường cao vẽ từ đỉnh của mỗi mặt bên (tam giác cân) xuống cạnh đáy của tam giác đó gọi là trung đoạn của hình chóp tam giác đều. Tất cả các trung đoạn của hình chóp tam giác đều có độ dài bằng nhau.
2. Tính chất của hình chóp tam giác đều
Hình chóp tam giác đều sở hữu những tính chất quan trọng, giúp chúng ta dễ dàng nhận biết và tính toán các yếu tố liên quan:
- Đáy là tam giác đều: Đây là yếu tố then chốt để xác định một hình chóp có phải là hình chóp tam giác đều hay không. Ba cạnh của tam giác đáy bằng nhau và ba góc của tam giác đáy bằng 60 độ.
- Mặt bên là các tam giác cân bằng nhau: Các mặt bên đều là những tam giác cân có đỉnh chung là đỉnh của hình chóp. Các cạnh bên của hình chóp (cạnh nối đỉnh với các đỉnh của đáy) có độ dài bằng nhau.
- Chân đường cao: Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của tam giác đáy. Điểm này chính là trọng tâm của tam giác đều.
3. Công thức tính diện tích xung quanh và thể tích
3.1. Diện tích xung quanh
Diện tích xung quanh của hình chóp tam giác đều là tổng diện tích của các mặt bên (ba tam giác cân). Công thức tính diện tích xung quanh như sau:
Sxq = p.d
Trong đó:
plà nửa chu vi đáy (nửa chu vi của tam giác đều).dlà trung đoạn của hình chóp.
3.2. Thể tích
Thể tích của hình chóp tam giác đều được tính bằng một phần ba tích của diện tích mặt đáy và chiều cao của hình chóp.
V = (1/3)S.h
Trong đó:
Slà diện tích đáy (diện tích của tam giác đều).hlà chiều cao của hình chóp (khoảng cách từ đỉnh đến mặt đáy).
4. Bài tập vận dụng
4.1. Bài tập nhận biết và tính toán yếu tố
Bài tập: Cho hình chóp tam giác đều S.DEF có đỉnh S, đáy DEF là tam giác đều cạnh 6cm, đường cao SO = 5cm. Gọi I là trung điểm của EF.
a) Xác định các yếu tố của hình chóp: đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao, trung đoạn.
b) Tính diện tích tam giác DEF.
c) Tính thể tích hình chóp S.DEF.
Giải:
a) Các yếu tố của hình chóp:
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Mặt bên: Tam giác SDE, SEF, SDF
- Mặt đáy: Tam giác DEF
- Đường cao: SO
- Một trung đoạn: SI
b) Vì tam giác DEF đều nên DE = EF = FD = 6 cm.
SI là đường cao của tam giác đều DEF, ta có:
SI = (cạnh căn(3)) / 2 = (6 căn(3)) / 2 = 3 * căn(3) cm.
Diện tích tam giác DEF là:
S = (1/2) EF SI = (1/2) 6 3 căn(3) = 9 căn(3) cm2.
c) Thể tích hình chóp S.DEF là:
V = (1/3) S SO = (1/3) 9 căn(3) 5 = 15 căn(3) cm3.
4.2. Bài tập ứng dụng thực tế
Bài tập: Một chiếc đèn trang trí có dạng hình chóp tam giác đều, mỗi mặt của đèn là một tam giác đều có cạnh bằng 20 cm. Tính diện tích giấy màu tối thiểu cần dùng để làm các mặt bên của đèn (bỏ qua diện tích mép gấp).
Giải:
Gọi H là trung điểm của AB (AB là một cạnh của tam giác đáy). SH là trung đoạn của hình chóp tam giác đều.
Ta có AH = HB = 20 : 2 = 10 (cm).
Sử dụng định lí Pythagore trong tam giác vuông SAH, ta suy ra
SH2 = SA2 – AH2 = 202 – 102 = 300.
Suy ra SH = căn(300) ≈ 17,32 cm.
Nửa chu vi mặt đáy ABC là:
p = (1/2)(20 + 20 + 20) = 30 cm.
Tổng diện tích các mặt bên của hình chóp đều là:
Sxq = p . SH = 30 . 17,32 = 519,6 cm2.
Vậy diện tích giấy màu tối thiểu cần sử dụng là 519,6 cm2.
5. Tổng kết
Hình chóp tam giác đều là một hình học không gian quan trọng với nhiều ứng dụng trong thực tế. Việc nắm vững định nghĩa, tính chất và công thức tính toán sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và chính xác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về hình chóp tam giác đều.