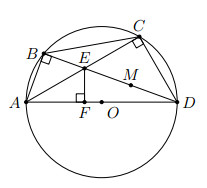
Cho Tứ Giác Abcd Nội Tiếp đường Tròn đường Kính Ad. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng:
a) Tứ giác ABEF, DCEF nội tiếp được.
b) Tia CA là tia phân giác của góc BCE.
c) Tứ giác BCMF nội tiếp được.
Lời giải:
a) Chứng minh tứ giác ABEF, DCEF nội tiếp được:
- Tứ giác ABEF:
- Ta có: $angle AEF = 90^circ$ (do EF vuông góc với AD)
- $angle ABD = 90^circ$ (góc nội tiếp chắn nửa đường tròn đường kính AD)
- Suy ra $angle AEF + angle ABE = 90^circ + 90^circ = 180^circ$
- Vậy tứ giác ABEF nội tiếp được (tứ giác có tổng hai góc đối bằng 180 độ).
Ảnh minh họa tứ giác ABEF nội tiếp, với ABCD nội tiếp đường tròn đường kính AD, EF vuông góc AD.
- Tứ giác DCEF:
- Ta có: $angle AEF = 90^circ$ (do EF vuông góc với AD)
- $angle ACD = 90^circ$ (góc nội tiếp chắn nửa đường tròn đường kính AD)
- $angle ACD$ và $angle FCE$ là hai góc đối đỉnh nên $angle FCE = 90^circ$.
- Suy ra $angle DEF + angle DCF = 90^circ + 90^circ = 180^circ$
- Vậy tứ giác DCEF nội tiếp được (tứ giác có tổng hai góc đối bằng 180 độ).
b) Chứng minh tia CA là tia phân giác của góc BCE:
- Vì tứ giác ABEF nội tiếp (chứng minh trên) nên $angle CAF = angle BEF$ (hai góc nội tiếp cùng chắn cung EF).
- Vì tứ giác DCEF nội tiếp (chứng minh trên) nên $angle CDE = angle CFE$ (hai góc nội tiếp cùng chắn cung CE).
- Xét tam giác AED vuông tại E có EF là đường cao nên $angle BEF = angle CDE$ (cùng phụ với góc AED).
- Từ đó suy ra $angle CAF = angle CDE$. Hay $angle EBA = angle EBC$
- Vậy CA là tia phân giác của góc BCE.
Hình vẽ minh họa chứng minh CA là tia phân giác góc BCE, với tứ giác ABCD nội tiếp trong đường tròn đường kính AD.
c) Chứng minh tứ giác BCMF nội tiếp được:
- Vì M là trung điểm của DE nên ME = MD. Suy ra tam giác MEF cân tại M nên $angle MFE = angle MEF$.
- Mà $angle MEF = angle CDE$ (vì tứ giác DCEF nội tiếp).
- Ta có: $angle CBM = angle CAD$ (hai góc nội tiếp cùng chắn cung CD).
- Ta cần chứng minh $angle CFM = angle CBM$ hay $angle CFM = angle CAD$.
- Lại có: $angle CAD = angle CDE = angle MFE = angle CFM$.
- Vậy tứ giác BCMF nội tiếp được (tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện).
Minh họa tứ giác BCMF nội tiếp đường tròn, với ABCD là tứ giác nội tiếp đường tròn đường kính AD và M là trung điểm DE.