Tính Góc Giữa Hai Mặt Phẳng Trong Tứ Diện Vuông: SA, SB, SC Đôi Một Vuông Góc

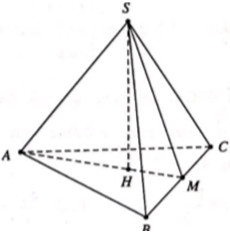
Bài toán về cho tứ diện S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau là một dạng bài hình học không gian thường gặp trong chương trình Toán THPT và các kỳ thi quan trọng. Dưới đây là một ví dụ cụ thể về cách giải quyết bài toán này, tập trung vào việc tính góc giữa hai mặt phẳng.

Đề bài:

Cho tứ diện S.ABC có SA, SB, SC đôi một vuông góc và SA = SB = SC = 1. Tính cosα, trong đó α là góc giữa mặt phẳng (SBC) và mặt phẳng (ABC).

Lời giải:

Để giải bài toán này, chúng ta sẽ sử dụng phương pháp hình học không gian kết hợp với kiến thức về tích vô hướng và tích có hướng của các vectơ.

1. Xác định các yếu tố vuông góc: Vì SA, SB, SC đôi một vuông góc, ta có thể xem S là gốc tọa độ của một hệ trục tọa độ Oxyz, với SA nằm trên trục Ox, SB nằm trên trục Oy, và SC nằm trên trục Oz.

2. Tìm tọa độ các điểm:

   • S(0; 0; 0)
   • A(1; 0; 0)
   • B(0; 1; 0)
   • C(0; 0; 1)

3. Tìm vectơ pháp tuyến của các mặt phẳng:

   • Mặt phẳng (SBC): Vectơ pháp tuyến là tích có hướng của hai vectơ SB và SC.
     SB = (0, 1, 0)
SC = (0, 0, 1)
     => n_(SBC) = [SB, SC] = (1; 0; 0)

   Alt text: Hình vẽ minh họa tứ diện S.ABC với SA, SB, SC đôi một vuông góc, thể hiện vectơ SB và SC nằm trên mặt phẳng (SBC) và vectơ pháp tuyến của (SBC)

   • Mặt phẳng (ABC): Để tìm vectơ pháp tuyến của (ABC), ta tìm tích có hướng của hai vectơ AB và AC.
     AB = (-1, 1, 0)
AC = (-1, 0, 1)
     => n_(ABC) = [AB, AC] = (1; 1; 1)

4. Tính cosin góc giữa hai mặt phẳng:

   Công thức tính cosin góc giữa hai mặt phẳng (SBC) và (ABC) là:

   cos(α) = |(n_(SBC) . n_(ABC))| / (|n_(SBC)| * |n_(ABC)|)

   Thay số:

   cos(α) = |(1 1 + 0 1 + 0 1)| / (√(1² + 0² + 0²) √(1² + 1² + 1²))

   cos(α) = |1| / (1 * √3)

   cos(α) = 1 / √3 = √3 / 3

Vậy, cosα = √3 / 3.

Alt text: Hình vẽ thể hiện cách xác định vectơ pháp tuyến của mặt phẳng (ABC) từ hai vectơ AB và AC, và cách sử dụng tích vô hướng để tính góc giữa hai mặt phẳng.

Mở rộng và ứng dụng:

Bài toán cho tứ diện S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau không chỉ dừng lại ở việc tính góc giữa hai mặt phẳng. Nó còn có thể mở rộng ra nhiều dạng toán khác như:

• Tính thể tích tứ diện.
• Tìm hình chiếu của một điểm lên một mặt phẳng.
• Chứng minh các tính chất hình học liên quan đến các yếu tố vuông góc.

Việc nắm vững phương pháp giải và các kiến thức liên quan sẽ giúp học sinh tự tin giải quyết các bài toán hình học không gian một cách hiệu quả.