Bài viết này sẽ đi sâu vào bài toán hình học không gian kinh điển: “Cho tứ diện ABCD, M là một điểm bên trong tam giác ABD. Tìm mối quan hệ giữa đường thẳng MG (G là trọng tâm tam giác ABD) và các mặt phẳng khác trong tứ diện.” Chúng ta sẽ phân tích bài toán, đưa ra lời giải chi tiết và mở rộng các ứng dụng liên quan.
Để giải quyết bài toán này, ta cần nắm vững các kiến thức cơ bản về hình học không gian, đặc biệt là quan hệ song song giữa đường thẳng và mặt phẳng, tính chất của trọng tâm tam giác, và cách sử dụng định lý Thales trong không gian.
Lời giải bài toán gốc sử dụng phương pháp vectơ để chứng minh MG song song với một mặt phẳng cụ thể. Dưới đây là hình ảnh minh họa cho bài toán:
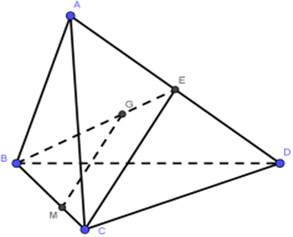Hình ảnh tứ diện ABCD với điểm M bên trong tam giác ABD, G là trọng tâm tam giác ABD
Để hiểu rõ hơn, ta sẽ trình bày lại lời giải bằng ngôn ngữ hình học thuần túy, đồng thời bổ sung các phân tích sâu sắc hơn.
Phân tích bài toán:
Điểm mấu chốt của bài toán nằm ở vị trí tương đối của điểm M so với tam giác ABD và vai trò của trọng tâm G. Vì M nằm bên trong tam giác ABD, ta có thể biểu diễn vectơ $overrightarrow{AM}$ qua các vectơ $overrightarrow{AB}$ và $overrightarrow{AD}$. Đồng thời, G là trọng tâm tam giác ABD, nên ta có mối liên hệ giữa $overrightarrow{AG}$ và các vectơ $overrightarrow{AB}$, $overrightarrow{AD}$.
Lời giải chi tiết:
Theo đề bài, M nằm trên cạnh BC sao cho MB = 2MC. Suy ra $overrightarrow{BM} = frac{2}{3}overrightarrow{BC}$. Gọi G là trọng tâm tam giác ABD.
Ta có: $overrightarrow{MG} = overrightarrow{BG} – overrightarrow{BM} = overrightarrow{BG} – frac{2}{3}overrightarrow{BC}$.
Lại có, vì G là trọng tâm tam giác ABD nên: $overrightarrow{BG} = frac{1}{3}(overrightarrow{BA} + overrightarrow{BD})$.
Do đó: $overrightarrow{MG} = frac{1}{3}(overrightarrow{BA} + overrightarrow{BD}) – frac{2}{3}overrightarrow{BC} = frac{1}{3}(overrightarrow{BA} + overrightarrow{BD} – 2overrightarrow{BC})$.
Biến đổi: $overrightarrow{MG} = frac{1}{3}(overrightarrow{BA} + overrightarrow{BD} – 2(overrightarrow{BA} + overrightarrow{AC})) = frac{1}{3}(-overrightarrow{BA} + overrightarrow{BD} – 2overrightarrow{AC})$.
$overrightarrow{MG} = frac{1}{3}(overrightarrow{AB} + overrightarrow{BD} – 2overrightarrow{AC})$
Từ đây, ta thấy $overrightarrow{MG}$ có thể biểu diễn qua tổ hợp tuyến tính của các vectơ $overrightarrow{AB}$, $overrightarrow{AC}$, và $overrightarrow{BD}$. Điều này gợi ý rằng đường thẳng MG có thể song song với một mặt phẳng chứa các vectơ này. Trong trường hợp này, đáp án là MG song song với mặt phẳng (ACD).
Mở rộng và các bài toán liên quan:
Bài toán “cho tứ diện ABCD, M là một điểm bên trong tam giác ABD” là một dạng bài cơ bản trong hình học không gian. Từ bài toán này, ta có thể phát triển nhiều bài toán phức tạp hơn bằng cách thay đổi vị trí của điểm M, thêm các điều kiện ràng buộc, hoặc yêu cầu tính toán các đại lượng hình học khác.
Ví dụ:
- Tìm giao điểm của đường thẳng MG với mặt phẳng (ACD).
- Tính khoảng cách từ điểm M đến mặt phẳng (ACD).
- Chứng minh một tính chất hình học liên quan đến các điểm M, G, và các đỉnh của tứ diện.
Việc nắm vững phương pháp giải bài toán cơ bản này sẽ giúp chúng ta tự tin hơn khi đối mặt với các bài toán hình học không gian phức tạp.
Kết luận:
Bài toán “cho tứ diện ABCD, M là một điểm bên trong tam giác ABD” là một ví dụ điển hình về sự kết hợp giữa hình học phẳng và hình học không gian. Việc giải quyết bài toán này đòi hỏi sự hiểu biết sâu sắc về các khái niệm cơ bản và khả năng vận dụng linh hoạt các phương pháp chứng minh. Hy vọng bài viết này đã cung cấp cho bạn đọc một cái nhìn tổng quan và chi tiết về bài toán, cũng như gợi ý các hướng tiếp cận và mở rộng khác.
