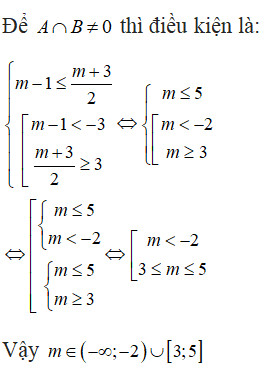Bài toán quen thuộc trong chương trình Toán lớp 10 là tìm điều kiện để giao của hai tập hợp khác rỗng. Bài viết này sẽ đi sâu vào một dạng toán cụ thể: cho tập hợp A là một khoảng và tập hợp B là hợp của hai khoảng, tìm tham số để A và B có giao khác rỗng. Điều kiện Cho Tập Hợp A Khác Rỗng đóng vai trò then chốt trong việc xác định các giá trị hợp lệ của tham số.
Xét bài toán: Cho tập hợp A = (m-1; m+3/2) và B = (-∞; -3) ∪ [3; +∞). Tìm tập hợp các giá trị thực của m để A ∩ B ≠ ∅.
Để giải quyết bài toán này, ta cần xét các trường hợp vị trí tương đối của khoảng A so với hai khoảng con của B. Điều quan trọng là phải đảm bảo cho tập hợp A khác rỗng, tức là độ dài của khoảng (m-1; m+3/2) phải lớn hơn 0. Điều này luôn đúng vì (m+3/2) – (m-1) = 5/2 > 0.
Ta xét các trường hợp sau:
- Trường hợp 1: A giao với (-∞; -3) khác rỗng. Điều này xảy ra khi m – 1 < -3, tức là m < -2.
- Trường hợp 2: A giao với [3; +∞) khác rỗng. Điều này xảy ra khi m + 3/2 > 3, tức là m > 3/2.
Vậy, để A ∩ B ≠ ∅, thì m < -2 hoặc m > 3/2.
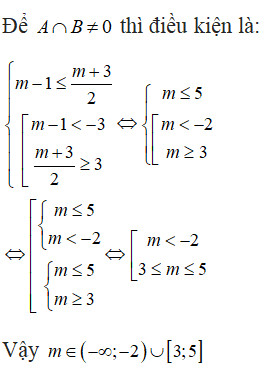{width=269 height=372}Ảnh minh họa trực quan cho thấy khoảng A=(m-1; m+3/2) có phần giao khác rỗng với tập hợp B là hợp của hai nửa khoảng số (-∞; -3) và [3; +∞), thể hiện điều kiện để bài toán có nghiệm. Điều này trực quan hóa khái niệm A ∩ B ≠ ∅.
Lưu ý: Điều kiện cho tập hợp A khác rỗng là một điều kiện cần, nhưng trong trường hợp này nó luôn đúng nên không ảnh hưởng đến kết quả cuối cùng. Tuy nhiên, trong các bài toán khác, việc kiểm tra điều kiện này là rất quan trọng. Ví dụ, nếu A = (m-1; m+1) và điều kiện là A khác rỗng, ta phải có (m+1) – (m-1) > 0, tức là 2 > 0 (luôn đúng). Nhưng nếu A = [m-1; m+1] và chỉ xét các giá trị nguyên của m, thì điều kiện A khác rỗng vẫn phải được xem xét để đảm bảo có ít nhất một phần tử trong A.
Ví dụ khác, nếu A = [m; m], thì A chỉ chứa một phần tử (nếu có) và để A khác rỗng thì m phải là một số xác định. Nếu m là một biểu thức phụ thuộc vào một biến khác, ta cần xét điều kiện để m tồn tại.
Trong bài toán tổng quát, khi cho tập hợp A khác rỗng và A được định nghĩa bởi một biểu thức chứa tham số, ta cần kiểm tra:
- Biểu thức định nghĩa A có nghĩa với những giá trị nào của tham số?
- Với những giá trị tham số làm cho biểu thức có nghĩa, A có thực sự khác rỗng không?
Việc bỏ qua điều kiện này có thể dẫn đến kết quả sai.
Ví dụ, xét bài toán tìm m để phương trình f(x) = 0 có nghiệm, với f(x) = (m-1)x + m. Nếu m = 1, f(x) = 1 ≠ 0, phương trình vô nghiệm. Nhưng nếu không xét điều kiện m-1 ≠ 0 (tương ứng với việc xét A khác rỗng, với A là tập nghiệm của phương trình), ta có thể bỏ sót trường hợp này.
Tóm lại, khi giải các bài toán liên quan đến tập hợp, đặc biệt là khi cho tập hợp A khác rỗng và A được định nghĩa bởi một biểu thức chứa tham số, cần kiểm tra cẩn thận các điều kiện để đảm bảo tính đúng đắn của kết quả. Việc này bao gồm việc xác định miền xác định của biểu thức và kiểm tra xem A có thực sự khác rỗng hay không.