Bài toán về tam giác ABC vuông cân tại A và điểm M nằm trong tam giác là một dạng bài hình học phổ biến, thường xuất hiện trong các kỳ thi và kiểm tra. Bài viết này sẽ đi sâu vào phân tích các tính chất, đặc điểm liên quan đến cấu hình hình học này, đồng thời mở rộng các hướng tiếp cận và ứng dụng của bài toán.
Xét tam giác ABC vuông cân tại A, ta có AB = AC và góc BAC = 90 độ. Khi đó, góc ABC = góc ACB = 45 độ. Việc xác định vị trí điểm M bên trong tam giác ABC sẽ tạo ra nhiều bài toán khác nhau, đòi hỏi các kỹ năng chứng minh hình học tổng hợp.
Một số bài toán thường gặp liên quan đến tam giác ABC vuông cân tại A và điểm M:
- Chứng minh các đoạn thẳng bằng nhau.
- Chứng minh các góc bằng nhau.
- Xác định vị trí điểm M thỏa mãn một điều kiện nào đó.
- Tính diện tích các hình tạo bởi điểm M và các đỉnh của tam giác.
Để giải quyết các bài toán này, chúng ta thường sử dụng các phương pháp sau:
- Chứng minh tam giác bằng nhau: Sử dụng các trường hợp bằng nhau của tam giác (cạnh-cạnh-cạnh, cạnh-góc-cạnh, góc-cạnh-góc, cạnh huyền – cạnh góc vuông, cạnh huyền – góc nhọn).
- Sử dụng tính chất của tam giác cân, tam giác vuông: Các góc ở đáy bằng nhau, định lý Pitago.
- Sử dụng tính chất đường phân giác, đường trung trực, đường trung tuyến: Các đường này có những tính chất đặc biệt giúp chứng minh các yếu tố hình học.
- Sử dụng các phép biến hình: Phép đối xứng trục, phép quay.
Ví dụ, nếu M là giao điểm của các đường phân giác trong tam giác ABC, ta có thể chứng minh được MA = MB = MC khi tam giác ABC vuông cân tại A.
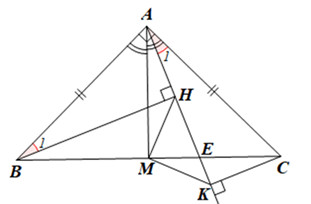Tam giác ABC cân tại A, AM là tia phân giác
Alt text: Hình ảnh tam giác ABC vuông cân tại A, có AM là tia phân giác của góc BAC, minh họa bài toán hình học.
Phân tích hình vẽ trên:
Hình vẽ minh họa tam giác ABC vuông cân tại A và AM là tia phân giác của góc BAC. Từ đó, ta có thể suy ra một số tính chất quan trọng:
- AM là đường phân giác của góc BAC nên góc BAM = góc CAM = 45 độ.
- Do tam giác ABC cân tại A nên đường phân giác AM cũng đồng thời là đường trung tuyến, đường cao và đường trung trực của cạnh BC.
Mở rộng bài toán:
Ngoài các bài toán cơ bản, chúng ta có thể mở rộng bài toán bằng cách thêm các yếu tố khác như đường tròn, các điểm đặc biệt khác (trọng tâm, trực tâm,…). Việc này sẽ tạo ra các bài toán phức tạp hơn, đòi hỏi sự sáng tạo và khả năng vận dụng linh hoạt các kiến thức hình học.
Ứng dụng:
Các bài toán về tam giác ABC vuông cân tại A và điểm M không chỉ có giá trị trong học tập mà còn có ứng dụng trong thực tế, chẳng hạn như trong thiết kế kiến trúc, xây dựng, đo đạc và các lĩnh vực kỹ thuật khác.
Kết luận:
Bài toán về tam giác ABC vuông cân tại A và điểm M là một chủ đề thú vị và có nhiều ứng dụng trong hình học. Việc nắm vững các kiến thức cơ bản và các phương pháp giải toán sẽ giúp chúng ta giải quyết các bài toán một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về chủ đề này.
