Cho Tam Giác ABC Đều Có Cạnh Bằng A: Công Thức, Bài Tập và Ứng Dụng

Tam giác đều là một hình học quan trọng và thường gặp trong toán học. Bài viết này sẽ đi sâu vào các công thức, bài tập và ứng dụng liên quan đến tam giác ABC đều có cạnh bằng a.

Tam Giác Đều Là Gì?

Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau, mỗi góc có số đo là 60 độ.

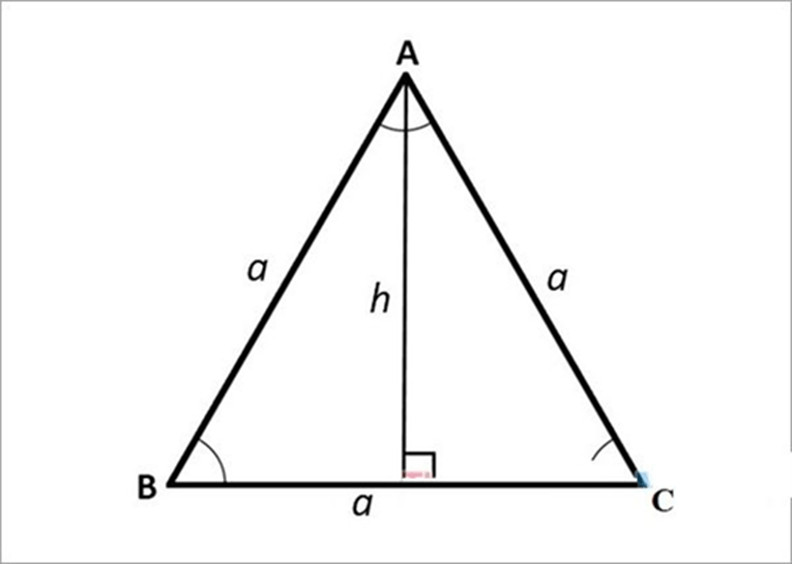
Tam giác đều ABC với các cạnh bằng nhau, minh họa khái niệm cơ bản về hình học tam giác.

Tính Chất Của Tam Giác Đều

Ba cạnh bằng nhau.
Ba góc bằng nhau (60 độ).
Đường cao, đường trung tuyến, đường phân giác, đường trung trực trùng nhau.
Có tính đối xứng cao.

Công Thức Tính Diện Tích Tam Giác Đều

Khi Cho Tam Giác Abc đều Có Cạnh Bằng A, ta có các công thức tính diện tích như sau:

Sử dụng chiều cao:
- Chiều cao (h) của tam giác đều được tính bằng công thức: h = (a√3) / 2
- Diện tích (S) được tính bằng: S = (1/2) * a * h = (a²√3) / 4
Sử dụng công thức Heron:
- Nửa chu vi (p) của tam giác đều là: p = (a + a + a) / 2 = (3a) / 2
- Diện tích (S) được tính bằng: S = √(p * (p - a) * (p - a) * (p - a)) = (a²√3) / 4

Công thức tính diện tích tam giác đều khi biết độ dài cạnh, giúp học sinh nắm vững kiến thức về hình học.

Ví Dụ Minh Họa

Ví dụ: Cho tam giác ABC đều có cạnh a = 4cm. Tính diện tích tam giác.

Giải:

Áp dụng công thức: S = (a²√3) / 4 = (4²√3) / 4 = (16√3) / 4 = 4√3 cm²

Các Dạng Bài Tập Thường Gặp Về Tam Giác Đều

Tính diện tích khi biết cạnh: Đây là dạng bài cơ bản, áp dụng trực tiếp công thức.
Tính cạnh khi biết diện tích: Biến đổi công thức để tìm cạnh a khi biết diện tích S.
Bài toán liên quan đến đường tròn nội tiếp/ngoại tiếp: Sử dụng các công thức liên quan đến bán kính đường tròn nội tiếp và ngoại tiếp của tam giác đều.

Ứng Dụng Của Tam Giác Đều

Tam giác đều xuất hiện nhiều trong thực tế và có nhiều ứng dụng quan trọng:

Kiến trúc và xây dựng: Sử dụng trong thiết kế các cấu trúc có tính ổn định cao.
Thiết kế đồ họa: Là một hình dạng cơ bản trong thiết kế và nghệ thuật.
Toán học và khoa học: Sử dụng trong các bài toán hình học, lượng giác và vật lý.

Các cách tiếp cận khác nhau để giải bài toán diện tích tam giác đều, giúp học sinh rèn luyện tư duy toán học.

Bài Tập Vận Dụng

Bài 1: Cho tam giác ABC đều có diện tích là 9√3 cm². Tính độ dài cạnh của tam giác.

Bài 2: Một khu vườn hình tam giác đều có cạnh dài 10m. Tính diện tích khu vườn.

Bài 3: Tính bán kính đường tròn nội tiếp và ngoại tiếp của tam giác ABC đều có cạnh a = 6cm.

Mở Rộng

Ngoài các công thức và bài tập cơ bản, bạn có thể tìm hiểu thêm về:

Các bài toán chứng minh liên quan đến tam giác đều.
Ứng dụng của tam giác đều trong các lĩnh vực khác nhau.
Mối liên hệ giữa tam giác đều và các hình học khác.

Hy vọng bài viết này cung cấp cho bạn đầy đủ kiến thức về cho tam giác abc đều có cạnh bằng a và giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.