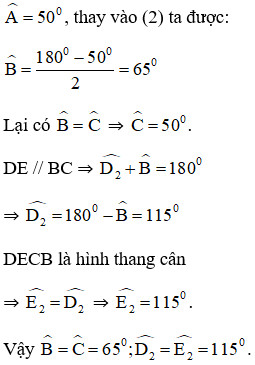Cho Tam Giác Abc Cân tại A. Trên các cạnh bên AB, AC lần lượt lấy các điểm D, E sao cho AD = AE. Bài toán này mở ra nhiều hướng khám phá thú vị về tính chất hình học, đặc biệt là liên quan đến hình thang cân.
a) Chứng minh rằng BDEC là hình thang cân.
Để chứng minh BDEC là hình thang cân, ta cần chứng minh hai điều: BDEC là hình thang và nó có hai góc ở đáy bằng nhau.
Xét tam giác ABC cân tại A, ta có AB = AC và góc B bằng góc C. Vì AD = AE nên tam giác ADE cũng cân tại A, suy ra góc ADE bằng góc AED.
Ta có góc ADE = (180° – góc A) / 2 và góc ABC = (180° – góc A) / 2. Do đó, góc ADE = góc ABC. Mà hai góc này ở vị trí đồng vị nên DE // BC. Từ đây suy ra tứ giác BDEC là hình thang.
Hình ảnh minh họa bài toán tam giác ABC cân với các điểm D, E trên AB và AC, giúp hình dung và hiểu rõ hơn đề bài.
Để chứng minh BDEC là hình thang cân, ta cần chứng minh góc B bằng góc C (đã có do tam giác ABC cân) hoặc chứng minh góc EDB bằng góc DEC. Vì DE // BC nên góc EDB = góc DBC và góc DEC = góc ECB. Do góc ABC = góc ACB (tam giác ABC cân) nên góc DBC = góc ECB. Vậy, góc EDB = góc DEC.
Vậy, BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng góc A = 50°.
Vì tam giác ABC cân tại A và góc A = 50° nên góc B = góc C = (180° – 50°) / 2 = 65°.
Hình ảnh thể hiện các góc của tam giác ABC cân và hình thang cân BDEC, giúp dễ dàng tính toán và hiểu rõ mối quan hệ giữa chúng.
Vì DE // BC nên góc ADE + góc DBE = 180°. Suy ra, góc DBE = 180° – góc ADE. Ta đã biết góc ADE = (180° – 50°) / 2 = 65°. Vậy góc DBE = 180° – 65° = 115°.
Do đó, góc DEC = 115° (vì BDEC là hình thang cân).
Vậy, các góc của hình thang cân BDEC là: góc B = góc C = 65° và góc EDB = góc DEC = 115°.
Hình ảnh minh họa hình thang cân BDEC với các góc đã được tính toán, giúp người đọc kiểm tra và đối chiếu kết quả.
Bài toán này là một ví dụ điển hình về ứng dụng tính chất của tam giác ABC cân để giải quyết các bài toán hình học phức tạp hơn. Việc hiểu rõ các định lý và tính chất liên quan đến tam giác cân và hình thang cân là rất quan trọng trong quá trình học tập và giải toán.