Bài toán tìm mô-đun của số phức là một dạng bài thường gặp trong chương trình Toán học phổ thông và các kỳ thi quan trọng. Để giải quyết dạng bài này, chúng ta cần nắm vững các kiến thức cơ bản về số phức, phép toán trên số phức và đặc biệt là khái niệm mô-đun của số phức. Dưới đây là một ví dụ điển hình:
Đề bài: Cho Số Phức Z Thỏa Mãn z(1-2i) + zi = 15 + i. Tìm môđun của số phức z.
Lời giải:
Để giải bài toán này, ta thực hiện các bước sau:
- Đặt z = a + bi, với a, b là các số thực. Đây là bước khởi đầu quan trọng, giúp chúng ta chuyển đổi biểu thức phức tạp về các phương trình đại số quen thuộc.
- Thay vào biểu thức đã cho: Thay z = a + bi vào phương trình z(1-2i) + zi = 15 + i, ta được:
(a + bi)(1 – 2i) + (a – bi)i = 15 + i - Khai triển và rút gọn: Thực hiện phép nhân và thu gọn các số hạng, ta có:
a + bi – 2ai – 2bi² + ai – bi² = 15 + i
a + bi – 2ai + 2b + ai + b = 15 + i
(a + 3b) + (-a + b)i = 15 + i - Đồng nhất hệ số: Từ phương trình trên, ta có hệ phương trình sau:
a + 3b = 15
-a + b = 1 - Giải hệ phương trình: Giải hệ phương trình này, ta tìm được giá trị của a và b. Cộng hai phương trình, ta được:
4b = 16 => b = 4
Thay b = 4 vào phương trình -a + b = 1, ta được:
-a + 4 = 1 => a = 3 - Tìm số phức z: Vậy số phức z = 3 + 4i.
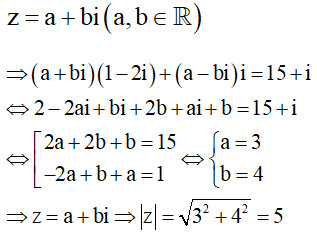Giải chi tiết bài toán tìm mô-đun số phức z thỏa mãn z(1-2i) + zi = 15 + i
- Tính mô-đun của z: Mô-đun của số phức z = a + bi được tính theo công thức |z| = √(a² + b²). Trong trường hợp này, ta có:
|z| = √(3² + 4²) = √(9 + 16) = √25 = 5
Kết luận: Vậy mô-đun của số phức z là 5.
Một số lưu ý khi giải bài toán “cho số phức z thỏa mãn…”:
- Nắm vững định nghĩa: Luôn nhớ định nghĩa số phức z = a + bi và mô-đun của nó |z| = √(a² + b²).
- Biến đổi linh hoạt: Sử dụng các phép toán trên số phức một cách linh hoạt để đơn giản hóa biểu thức.
- Kiểm tra kết quả: Sau khi tìm được số phức z, hãy thay lại vào phương trình ban đầu để kiểm tra tính chính xác.
Các dạng bài tập thường gặp khác liên quan đến “cho số phức z thỏa mãn”:
- Tìm phần thực, phần ảo của số phức z.
- Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ.
- Tìm số phức z thỏa mãn đồng thời nhiều điều kiện.
Việc luyện tập thường xuyên với nhiều dạng bài khác nhau sẽ giúp bạn nâng cao kỹ năng giải toán và tự tin hơn khi đối mặt với các bài toán về số phức. Chúc các bạn học tốt!
