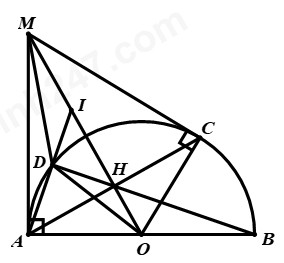
a) Chứng minh A, O, C, M cùng thuộc một đường tròn.
Xét bài toán quen thuộc: cho nửa đường tròn tâm O đường kính AB=2R, trên nửa đường tròn lấy điểm C. Từ một điểm M nằm ngoài đường tròn (O), kẻ các tiếp tuyến MA, MC đến đường tròn (O) (A, C là các tiếp điểm). Chứng minh rằng các điểm A, O, C, M cùng thuộc một đường tròn.
Chứng minh:
MA là tiếp tuyến của đường tròn (O) => MA ⊥ AO => ΔMAO vuông tại A => A thuộc đường tròn đường kính MO. Chứng minh điều này giúp ta hiểu rõ hơn về tính chất tiếp tuyến và đường tròn ngoại tiếp.
MC là tiếp tuyến của đường tròn (O) => MC ⊥ CO => ΔMCO vuông tại C => C thuộc đường tròn đường kính MO.
Do đó, A, C thuộc đường tròn đường kính MO => A, O, C, M cùng thuộc một đường tròn. Từ đây ta có thể suy ra nhiều tính chất hình học quan trọng khác.
b) Chứng minh OH.OM = R²
Chứng minh hệ thức liên quan đến bán kính R, đoạn OH và OM là một dạng toán thường gặp khi làm việc với đường tròn.
Chứng minh:
MA, MC là tiếp tuyến của đường tròn (O) tại A, C => MA = MC (tính chất hai tiếp tuyến cắt nhau). Lại có: OA = OC = R => MO là đường trung trực của AC => MO ⊥ AC.
Ta có: MO ⊥ AC (cmt); MO ∩ AC = {H} => AH ⊥ MO.
ΔMAO vuông tại A, AH ⊥ MO, áp dụng hệ thức lượng trong tam giác vuông: AO² = OH.OM.
Mà AO = R => OH.OM = R². Việc chứng minh hệ thức này có ứng dụng rất lớn trong các bài toán liên quan đến tính toán khoảng cách và chứng minh các điểm thẳng hàng.
c) Chứng minh ΔDOM ∼ ΔOHD
Chứng minh hai tam giác đồng dạng là một kỹ năng quan trọng trong hình học, nó giúp ta suy ra các tỉ lệ và góc bằng nhau.
Ta có: AO² = OH.OM (cmt) mà AO = DO = R
=> DO² = OH.OM
=> DO/OM = OH/DO
Xét ΔODM và ΔOHD có:
∠DOM chung
DO/OM = OH/DO
=> ΔDOM ∼ ΔOHD (c.g.c)
d) Chứng minh IM = IH
Chứng minh:
ΔODM ∼ ΔOHD (cmt) => ∠ODH = ∠OMD
Mà ∠ODH = ∠OBD (vì tam giác OBD cân tại O)
Ta có: ∠OBD = ∠DAM (cùng phụ với ∠DAB)
=> ∠DAM = ∠OMD
=> ∠IAM = ∠IMD
=> ΔIAM ∼ ΔIMD (g.g) => IA/IM = IM/ID => IM² = IA.ID
ΔIHA vuông tại H, HD là đường cao, áp dụng hệ thức lượng trong tam giác vuông, ta có: IH² = ID.IA
Vậy IM² = IH² = IA.ID => IM = IH
Mà I thuộc MH
=> I là trung điểm của MH. Điều này cho thấy sự liên hệ giữa các yếu tố khác nhau trong hình học, từ đó giúp chúng ta giải quyết các bài toán phức tạp hơn.