Bài viết này sẽ đi sâu vào một bài toán hình học kinh điển liên quan đến “Cho Nửa đường Tròn O đường Kính Ab”. Chúng ta sẽ xem xét các tính chất quan trọng và cách giải quyết bài toán một cách chi tiết.
Đề bài: Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
a) ∠COD = 90°.
b) CD = AC + BD.
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.
Lời giải chi tiết:
Bài toán này không chỉ là một bài tập hình học thông thường mà còn là cơ hội để hiểu sâu hơn về các tính chất của đường tròn và các đường tiếp tuyến. Hãy cùng phân tích từng phần của bài toán.
Theo đề bài, ta có:
OA ⊥ Ax, OB ⊥ By
Điều này cho thấy Ax và By là các tiếp tuyến của nửa đường tròn lần lượt tại A và B. Đây là một điểm quan trọng để bắt đầu bài giải.
Vì CA, CM là hai tiếp tuyến của (O) lần lượt tại A và M, theo tính chất hai tiếp tuyến cắt nhau, ta có: CM = CA và ∠O₁ = ∠O₂. Tương tự, vì DB, DM là hai tiếp tuyến của đường tròn (O) lần lượt tại B và M, theo tính chất hai tiếp tuyến cắt nhau, ta có: DM = DB và ∠O₃ = ∠O₄.
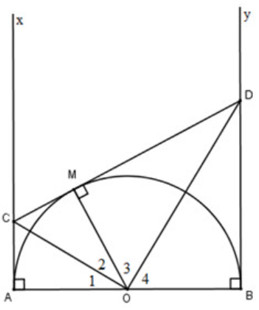Hình vẽ minh họa nửa đường tròn tâm O, đường kính AB, tiếp tuyến và các điểm liên quan
a) Chứng minh ∠COD = 90°:
Ta có:
∠O₁ + ∠O₂ + ∠O₃ + ∠O₄ = 180° (tổng các góc kề bù)
⇔ ∠O₂ + ∠O₂ + ∠O₃ + ∠O₃ = 180° (do ∠O₁ = ∠O₂ , ∠O₃ = ∠O₄)
⇔ 2∠O₂ + 2∠O₃ = 180°
⇔ ∠O₂ + ∠O₃ = 90°
⇔ ∠COD = 90° (điều phải chứng minh)
b) Chứng minh CD = AC + BD:
Ta đã chứng minh ở trên rằng CM = AC và MD = BD.
Lại có: CD = CM + MD = AC + BD (điều phải chứng minh)
c) Chứng minh tích AC.BD không đổi:
Ta có: CM = AC và MD = BD (chứng minh trên).
Xét tam giác COD vuông tại O (chứng minh ở phần a). Áp dụng hệ thức lượng trong tam giác vuông, ta có:
MO² = MC.MD = AC.BD = R² (do MO = R, bán kính của nửa đường tròn)
Vì bán kính R của đường tròn là một hằng số (không đổi) khi M di chuyển trên nửa đường tròn, nên tích AC.BD cũng không đổi. Đây chính là điều cần chứng minh.
Kết luận:
Bài toán về “cho nửa đường tròn o đường kính ab” không chỉ kiểm tra kiến thức về đường tròn và tiếp tuyến, mà còn rèn luyện khả năng vận dụng các hệ thức lượng trong tam giác vuông. Việc hiểu rõ các tính chất này sẽ giúp bạn giải quyết các bài toán hình học phức tạp hơn một cách dễ dàng.