Trong hình học phẳng, nửa đường tròn không chỉ là một hình dạng đơn giản mà còn chứa đựng nhiều tính chất và bài toán thú vị. Bài viết này sẽ đi sâu vào một bài toán điển hình liên quan đến nửa đường tròn, đồng thời mở rộng ra các ứng dụng và khái niệm liên quan.
Bài Toán Kinh Điển Về Nửa Đường Tròn
Cho Nửa đường Tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
a) Góc COD bằng 90 độ.
b) CD = AC + BD.
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.
Lời Giải Chi Tiết
Phân tích bài toán: Bài toán này kết hợp nhiều kiến thức hình học quan trọng như tiếp tuyến, góc nội tiếp, tam giác vuông và hệ thức lượng trong tam giác vuông. Việc chứng minh đòi hỏi sự linh hoạt trong việc áp dụng các định lý và tính chất.
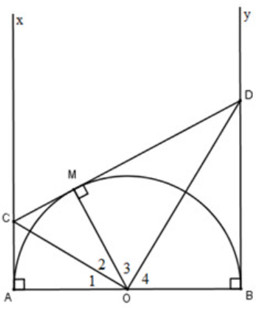Hình vẽ minh họa bài toán về nửa đường tròn
Alt text: Hình vẽ minh họa bài toán nửa đường tròn, đường kính AB, tiếp tuyến tại M cắt Ax và By tại C và D, thể hiện mối quan hệ giữa các đoạn thẳng và góc.
Chứng minh:
a) Chứng minh COD^=90o:
- Vì Ax và By vuông góc với AB, nên Ax và By là các tiếp tuyến của nửa đường tròn tại A và B.
- Theo tính chất hai tiếp tuyến cắt nhau, CA = CM và góc O1 = góc O2, tương tự DB = DM và góc O3 = góc O4 (ký hiệu góc O1, O2, O3, O4 như hình vẽ).
- Tổng các góc O1 + O2 + O3 + O4 = 180o (tổng các góc kề bù).
- Suy ra 2(O2 + O3) = 180o, do đó O2 + O3 = 90o. Vậy góc COD = 90o.
b) Chứng minh CD = AC + BD:
- Ta có CD = CM + MD.
- Mà CM = AC và MD = BD (chứng minh trên).
- Vậy CD = AC + BD.
c) Chứng minh tích AC.BD không đổi:
- Xét tam giác COD vuông tại O (chứng minh ở câu a).
- Áp dụng hệ thức lượng trong tam giác vuông: OM^2 = CM.MD = AC.BD.
- Vì OM là bán kính của nửa đường tròn (OM = R), nên AC.BD = R^2 (không đổi).
- Vậy tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.
Ứng Dụng và Mở Rộng
Bài toán “cho nửa đường tròn” không chỉ là một bài tập hình học đơn thuần mà còn là nền tảng cho nhiều bài toán phức tạp hơn. Các tính chất và kết quả thu được từ bài toán này có thể được áp dụng trong các lĩnh vực khác nhau như:
- Thiết kế kỹ thuật: Ứng dụng trong việc tính toán và thiết kế các cấu trúc hình học liên quan đến đường tròn và cung tròn.
- Kiến trúc: Sử dụng trong việc tạo ra các hình dạng và không gian kiến trúc độc đáo.
- Toán học cao cấp: Làm cơ sở cho các bài toán về quỹ tích, cực và đối cực trong hình học xạ ảnh.
Tổng Kết
Bài toán “cho nửa đường tròn” là một ví dụ điển hình về vẻ đẹp và sự sâu sắc của hình học phẳng. Việc nắm vững các tính chất và kỹ năng giải quyết bài toán này không chỉ giúp học sinh rèn luyện tư duy logic mà còn mở ra cánh cửa khám phá những kiến thức toán học thú vị hơn. Hãy tiếp tục khám phá và chinh phục những bài toán hình học khác để trau dồi kiến thức và kỹ năng của bạn.
