Cho khối hộp ABCD.A’B’C’D’ có thể tích V. Xét bài toán mặt phẳng (MB’D’) chia khối hộp thành hai phần, trong đó M là trung điểm cạnh AB. Mục tiêu là xác định thể tích phần khối đa diện chứa đỉnh A. Bài viết này sẽ trình bày chi tiết phương pháp giải quyết bài toán này, tập trung vào việc ứng dụng các tỉ lệ thể tích và tính chất hình học không gian.
Lời giải chi tiết cho bài toán như sau:
Gọi thể tích khối hộp ABCD.A’B’C’D’ là V. Theo đề bài, ta có V = 2018 (trong trường hợp tổng quát, ta sẽ ký hiệu thể tích là V).
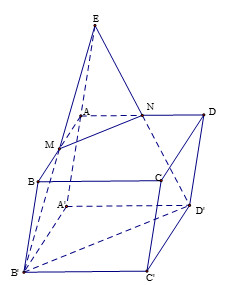Hình minh họa khối hộp ABCD.A'B'C'D' với mặt phẳng (MB'D') cắt và M là trung điểm AB
Để giải quyết bài toán, ta cần xác định giao điểm của mặt phẳng (MB’D’) với các cạnh của hình hộp. Gọi N là giao điểm của AD’ với mặt phẳng (MB’D’).
Ta có M là trung điểm của AB, suy ra M là trung điểm của EB’. Điều này dẫn đến N là trung điểm của ED’ và AD.
Tiếp theo, ta tính tỉ lệ thể tích của các khối đa diện được tạo ra.
Xét tỉ lệ thể tích của khối chóp A.MB’D’N so với thể tích khối hộp. Do N là trung điểm của AD’, ta có AN = (1/2)AD’. Vì M là trung điểm của AB, AM = (1/2)AB.
Khi đó, thể tích của khối chóp A.MB’D’N có thể được tính thông qua công thức tỉ lệ thể tích.
Từ các tỉ lệ trên, ta có thể suy ra thể tích của phần khối đa diện chứa đỉnh A. Cụ thể, thể tích phần chứa đỉnh A bằng V – V(MB’C’D’D), trong đó V(MB’C’D’D) là thể tích của khối đa diện chứa đỉnh C’.
Việc tính toán chi tiết thể tích V(MB’C’D’D) đòi hỏi việc phân tích kỹ lưỡng hơn về vị trí tương đối của các điểm và mặt phẳng. Tuy nhiên, với các thông tin đã có, ta có thể xác định được tỉ lệ thể tích và từ đó suy ra thể tích phần khối đa diện chứa đỉnh A theo V.
Kết luận:
Thể tích phần khối đa diện chứa đỉnh A có thể được tính thông qua việc xác định các tỉ lệ thể tích giữa các khối đa diện nhỏ được tạo ra bởi mặt phẳng (MB’D’). Kết quả cuối cùng sẽ là một biểu thức phụ thuộc vào thể tích V của khối hộp ABCD.A’B’C’D’.
