Thể Tích Khối Chóp Tứ Giác Đều S.ABCD: Bài Toán Điển Hình và Phương Pháp Giải

Bài viết này sẽ đi sâu vào dạng toán tính thể tích cho hình chóp tứ giác đều S.ABCD, một chủ đề quan trọng trong chương trình hình học không gian lớp 12 và thường xuyên xuất hiện trong các kỳ thi. Chúng ta sẽ cùng nhau phân tích một bài toán cụ thể, từ đó rút ra phương pháp giải tổng quát và hiệu quả.

Bài toán: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60°. Tính thể tích khối chóp S.ABCD.

Lời giải chi tiết:

Để giải bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về hình chóp tứ giác đều và các công thức tính thể tích liên quan.

1. Xác định các yếu tố của hình chóp tứ giác đều:

   • Đáy ABCD là hình vuông.
   • Các cạnh bên SA, SB, SC, SD bằng nhau.
   • Chân đường cao của hình chóp trùng với tâm O của đáy.

2. Tìm đường cao của hình chóp:

   Gọi O là tâm của hình vuông ABCD. Vì S.ABCD là hình chóp tứ giác đều, nên SO vuông góc với mặt phẳng (ABCD). Do đó, AO là hình chiếu vuông góc của SA lên mặt phẳng (ABCD). Góc giữa cạnh bên SA và mặt phẳng đáy (ABCD) là góc SAO. Theo đề bài, góc SAO = 60°.

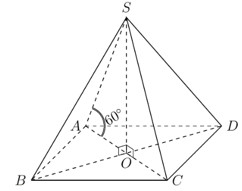   Hình chóp tứ giác đều S.ABCD với đường cao SO và góc SAO

   Hình ảnh minh họa hình chóp tứ giác đều S.ABCD, đường cao SO, tâm đáy O, và góc giữa cạnh bên SA và mặt đáy (ABCD) bằng 60 độ.

   Trong tam giác vuông SAO, ta có:

   • AO = (a√2)/2 (nửa đường chéo của hình vuông cạnh a)
   • SO = AO tan(SAO) = (a√2)/2 tan(60°) = (a√6)/2

3. Tính diện tích đáy:

   Diện tích đáy ABCD là:

   • S_ABCD = a²

4. Tính thể tích khối chóp:

   Thể tích khối chóp S.ABCD được tính theo công thức:

   • V = (1/3) SO S_ABCD = (1/3) (a√6)/2 a² = (a³√6)/6

Kết luận: Thể tích khối chóp tứ giác đều S.ABCD là (a³√6)/6. Đáp án C là chính xác.

Phương pháp giải tổng quát cho bài toán thể tích hình chóp tứ giác đều S.ABCD:

1. Xác định các yếu tố đã cho: Cạnh đáy, góc giữa cạnh bên và đáy, góc giữa mặt bên và đáy, hoặc các yếu tố khác.
2. Tìm đường cao: Sử dụng các mối quan hệ hình học, đặc biệt là các tam giác vuông, để tìm chiều cao của hình chóp.
3. Tính diện tích đáy: Đáy là hình vuông, nên diện tích đáy dễ dàng tính được khi biết cạnh đáy.
4. Áp dụng công thức: Sử dụng công thức V = (1/3) h S_đáy để tính thể tích.

Lưu ý:

• Việc xác định đúng góc giữa cạnh bên và mặt đáy, hoặc mặt bên và mặt đáy là rất quan trọng.
• Nắm vững các công thức lượng giác và các tính chất của hình vuông, tam giác vuông để giải quyết bài toán.

Bài viết này đã cung cấp một ví dụ cụ thể và phương pháp giải tổng quát cho hình chóp tứ giác đều S.ABCD. Hy vọng nó sẽ giúp bạn đọc hiểu rõ hơn về dạng toán này và áp dụng thành công trong các bài tập và kỳ thi. Chúc các bạn học tốt!