Cho hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, với AD = CD = a, AB = 2a, cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a. Dưới đây là phân tích chi tiết các phần của bài toán này.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
Để chứng minh (SAD) vuông góc (SDC), ta cần chứng minh một đường thẳng thuộc mặt phẳng (SAD) vuông góc với mặt phẳng (SDC). Vì SA vuông góc với mặt phẳng (ABCD), nên SA vuông góc với DC. Mặt khác, DC vuông góc với AD (do ABCD là hình thang vuông tại A và D). Vậy DC vuông góc với mặt phẳng (SAD). Do đó, (SAD) vuông góc (SDC).
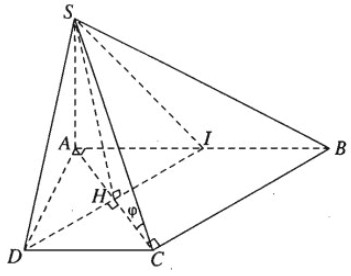Hình chóp S.ABCD với đáy là hình thang vuông ABCD
Hình ảnh minh họa hình chóp S.ABCD, đáy là hình thang vuông, SA vuông góc đáy, giúp hình dung trực quan các yếu tố và quan hệ hình học.
Gọi I là trung điểm của AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI song song với CB và DI vuông góc với CA nên AC vuông góc với CB. Do đó CB vuông góc với (SAC). Vậy (SBC) vuông góc (SAC).
Hình ảnh thể hiện các đường thẳng vuông góc và mối quan hệ giữa các mặt phẳng (SCD) và (SAD), làm rõ cơ sở chứng minh tính vuông góc.
b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.
Để tìm góc giữa hai mặt phẳng (SBC) và (ABCD), ta xác định giao tuyến của chúng là BC. Từ A kẻ đường thẳng vuông góc với BC tại H. Khi đó, góc giữa (SBC) và (ABCD) là góc SHA. Ta có tanφ = SA/AH. Tính AH dựa vào các yếu tố hình học của hình thang vuông ABCD.
Hình ảnh mô tả góc φ giữa (SBC) và (ABCD), cùng các yếu tố liên quan đến việc tính tanφ, hỗ trợ giải quyết bài toán tính góc.
c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α).
Mặt phẳng (α) chứa SD và vuông góc với (SAC) chính là mặt phẳng (SDI), với I là trung điểm của AB. Do đó, thiết diện của (α) với hình chóp S.ABCD là tam giác SDI. Để xác định rõ hơn, ta cần chứng minh SDI là tam giác gì.
Hình ảnh biểu diễn mặt phẳng (α) chứa SD và vuông góc (SAC), cùng thiết diện SDI tạo bởi (α) và hình chóp, giúp hình dung không gian và giải quyết bài toán thiết diện.
Gọi H là tâm hình vuông AICD ta có SH vuông góc DI và tính toán các yếu tố liên quan đến tam giác SDI. Diện tích tam giác SDI có thể được tính bằng công thức diện tích tam giác khi biết độ dài các cạnh.
Hình ảnh minh họa các bước tính diện tích thiết diện SDI, cung cấp công cụ trực quan để giải quyết phần tính toán diện tích.
