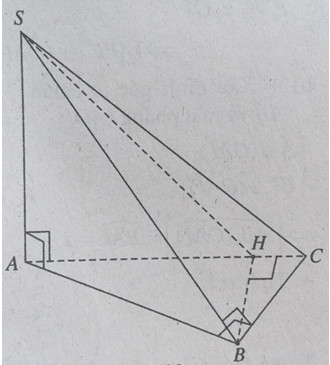
Xét bài toán hình học không gian với hình chóp S.ABC, trong đó đáy ABC là tam giác vuông tại B và cạnh SA vuông góc với mặt phẳng đáy (ABC). Bài toán này thường xuất hiện trong chương trình hình học lớp 11 và các kỳ thi quan trọng. Dưới đây là phân tích và giải chi tiết các phần của bài toán:
a) Chứng minh tam giác SBC vuông
Vì SA vuông góc với mặt phẳng (ABC), nên SA vuông góc với mọi đường thẳng nằm trong mặt phẳng (ABC). Do đó, SA vuông góc với BC.
Ta có:
- BC vuông góc với SA (do SA ⊥ (ABC))
- BC vuông góc với AB (do tam giác ABC vuông tại B)
Từ đó suy ra BC vuông góc với mặt phẳng (SAB). Vì SB nằm trong mặt phẳng (SAB) nên BC vuông góc với SB.
Vậy tam giác SBC vuông tại B.
Hình ảnh minh họa hình chóp S.ABC, đáy ABC là tam giác vuông tại B, SA vuông góc với đáy, dùng để trực quan hóa bài toán không gian.
b) Gọi H là chân đường cao vẽ từ B của tam giác ABC. Chứng minh (SAC) ⊥ (SBH)
Gọi H là chân đường cao kẻ từ B của tam giác ABC. Ta cần chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (SBH).
Ta có:
- BH vuông góc với AC (do BH là đường cao của tam giác ABC)
- BH vuông góc với SA (do SA vuông góc với mặt phẳng (ABC), mà BH nằm trong (ABC))
Suy ra BH vuông góc với mặt phẳng (SAC). Vì BH nằm trong mặt phẳng (SBH), nên mặt phẳng (SBH) vuông góc với mặt phẳng (SAC).
Vậy (SAC) ⊥ (SBH).
c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)
Để tính khoảng cách từ điểm B đến mặt phẳng (SAC), ta cần tìm độ dài đoạn BH, với H là hình chiếu vuông góc của B lên AC.
Trong tam giác vuông ABC, ta có:
1/BH² = 1/AB² + 1/BC² (Hệ thức lượng trong tam giác vuông)
Thay AB = a và BC = 2a vào, ta được:
1/BH² = 1/a² + 1/(2a)² = 1/a² + 1/4a² = 5/4a²
Suy ra BH² = 4a²/5, do đó BH = √(4a²/5) = 2a/√5 = (2a√5)/5
Vậy khoảng cách từ B đến mặt phẳng (SAC) là BH = (2a√5)/5.
Hình ảnh minh họa cách tính khoảng cách từ điểm B đến mặt phẳng (SAC), sử dụng hệ thức lượng trong tam giác vuông và biểu diễn các cạnh AB, BC, BH.
Bài toán về hình chóp S.ABC có đáy là tam giác vuông tại B, với SA vuông góc đáy, là một dạng bài tập điển hình trong chương trình hình học không gian. Việc nắm vững các kiến thức về đường thẳng vuông góc với mặt phẳng, mặt phẳng vuông góc với mặt phẳng, và hệ thức lượng trong tam giác vuông là rất quan trọng để giải quyết các bài toán tương tự.