Bài toán tìm khoảng cách giữa hai đường thẳng chéo nhau là một dạng bài quen thuộc trong chương trình hình học không gian lớp 11 và thường xuất hiện trong các kỳ thi quan trọng. Trong bài viết này, chúng ta sẽ xét một bài toán điển hình: cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, và tìm khoảng cách giữa hai đường thẳng AC và SD.
Đề bài:
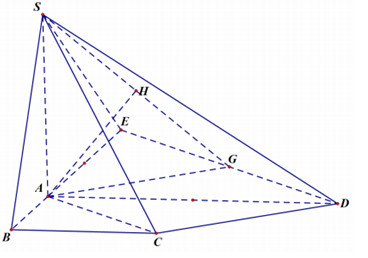
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh SA vuông góc với mặt phẳng đáy và SA = a. Tính theo a khoảng cách giữa hai đường thẳng AC và SD.
Lời giải:
Để giải quyết bài toán này, chúng ta sẽ sử dụng phương pháp tìm đường vuông góc chung của hai đường thẳng AC và SD.
Bước 1: Xác định các yếu tố hình học quan trọng
- ABCD là hình thang vuông tại A và B, nghĩa là AB vuông góc với AD và BC.
- SA vuông góc với mặt phẳng đáy (ABCD), suy ra SA vuông góc với mọi đường thẳng nằm trong mặt phẳng đáy, bao gồm AC và AD.
Bước 2: Tìm đường vuông góc chung
Đây là bước quan trọng nhất. Ta cần tìm một đoạn thẳng vừa vuông góc với AC, vừa vuông góc với SD. Thông thường, ta sẽ dựng các mặt phẳng phụ trợ hoặc sử dụng các tính chất hình học để xác định đoạn vuông góc chung này.
Bước 3: Tính độ dài đoạn vuông góc chung
Sau khi xác định được đoạn vuông góc chung, chúng ta cần tính độ dài của nó theo a. Việc này có thể sử dụng các hệ thức lượng trong tam giác, định lý Pythagoras, hoặc các phương pháp hình học khác.
Lưu ý khi giải bài toán:
- Vẽ hình chính xác và trực quan là yếu tố then chốt để giải quyết bài toán hình học không gian.
- Xác định đúng các yếu tố vuông góc và sử dụng chúng một cách hiệu quả.
- Nắm vững các công thức và định lý liên quan đến khoảng cách trong không gian.
- Có thể sử dụng phương pháp tọa độ hóa để giải bài toán, tuy nhiên, phương pháp hình học thuần túy thường mang lại cách giải ngắn gọn và đẹp mắt hơn.
Bài toán cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B và tính khoảng cách giữa hai đường thẳng AC và SD là một ví dụ điển hình về dạng toán khoảng cách trong hình học không gian. Việc nắm vững phương pháp giải và rèn luyện kỹ năng vẽ hình sẽ giúp bạn tự tin giải quyết các bài toán tương tự.