Thể Tích Khối Chóp Đều S.ABCD: Bài Toán Điển Hình và Phương Pháp Giải

Bài viết này sẽ tập trung vào dạng toán tính thể tích cho hình chóp đều S.ABCD, một chủ đề quan trọng trong chương trình hình học không gian. Chúng ta sẽ cùng phân tích một bài toán cụ thể, từ đó rút ra phương pháp giải tổng quát và các lưu ý quan trọng.

Bài Toán:

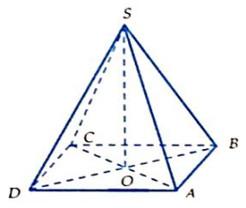
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, biết góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích V của khối chóp S.ABCD.

Phân Tích Bài Toán và Hướng Giải:

Để tính thể tích khối chóp S.ABCD, chúng ta cần xác định hai yếu tố chính:

1. Diện tích đáy: Vì S.ABCD là hình chóp đều, đáy ABCD là hình vuông.
2. Chiều cao: Chiều cao của hình chóp là đoạn thẳng SO, với O là tâm của hình vuông ABCD.

Góc giữa cạnh bên và mặt đáy là góc giữa cạnh bên (ví dụ SA) và hình chiếu của nó trên mặt đáy (là đoạn AO). Do đó, góc SAO = 45°. Từ đây, ta có thể tìm mối liên hệ giữa chiều cao SO và cạnh đáy a.

Lời Giải Chi Tiết:

1. Tính diện tích đáy:

   • Đáy ABCD là hình vuông cạnh a.
   • Diện tích đáy: S_ABCD = a²

2. Xác định chiều cao:

   • Gọi O là tâm của hình vuông ABCD.
   • Khi đó, AO là hình chiếu của SA trên mặt phẳng (ABCD).
   • Góc giữa SA và (ABCD) là góc SAO = 45°.
   • Tam giác SAO vuông tại O, có góc SAO = 45° nên là tam giác vuông cân tại O. Do đó, SO = AO.
   • Tính AO: Vì O là tâm hình vuông ABCD, AO là nửa đường chéo của hình vuông. Vậy AO = (a√2)/2.
   • Suy ra, SO = (a√2)/2.

3. Tính thể tích:

   • Thể tích khối chóp S.ABCD là: V = (1/3) S_ABCD SO = (1/3) a² (a√2)/2 = (a³√2)/6.

Vậy, thể tích V của khối chóp S.ABCD là (a³√2)/6.

Tổng Quát Hóa Phương Pháp Giải Bài Toán Cho Hình Chóp Đều S.ABCD:

1. Xác định đáy: Đáy của hình chóp đều S.ABCD luôn là hình vuông. Tính diện tích hình vuông dựa vào cạnh đáy (thường được cho trực tiếp hoặc gián tiếp qua các yếu tố khác).

2. Tìm tâm đáy: Tâm của hình vuông là giao điểm của hai đường chéo. Đây là điểm quan trọng để xác định đường cao của hình chóp.

3. Xác định chiều cao: Chiều cao của hình chóp là đoạn thẳng nối đỉnh S với tâm O của đáy. Để tính chiều cao, thường sử dụng các yếu tố sau:

   • Góc giữa cạnh bên và mặt đáy: Góc này thường cho phép thiết lập mối quan hệ giữa chiều cao và nửa đường chéo của đáy.
   • Góc giữa mặt bên và mặt đáy: Góc này liên quan đến đường cao của mặt bên và khoảng cách từ tâm đáy đến cạnh đáy.
   • Độ dài cạnh bên: Kết hợp với nửa đường chéo của đáy, ta có thể sử dụng định lý Pythagoras để tính chiều cao.

4. Tính thể tích: Áp dụng công thức V = (1/3) S_đáy h, trong đó h là chiều cao vừa tính được.

Các Lưu Ý Quan Trọng Khi Giải Bài Toán Về Hình Chóp Đều S.ABCD:

• Vẽ hình chính xác: Một hình vẽ rõ ràng và chính xác sẽ giúp bạn hình dung bài toán tốt hơn và tránh những sai sót không đáng có.
• Xác định đúng góc: Đọc kỹ đề bài để xác định đúng góc giữa các đường thẳng và mặt phẳng. Thường gặp là góc giữa cạnh bên và mặt đáy, góc giữa mặt bên và mặt đáy.
• Sử dụng các định lý và công thức phù hợp: Nắm vững các định lý Pythagoras, các công thức lượng giác trong tam giác vuông, và các công thức tính diện tích hình vuông.
• Kiểm tra kết quả: Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính hợp lý. Ví dụ, thể tích không thể là số âm.

Hy vọng với bài viết này, bạn đã nắm vững phương pháp giải bài toán tính thể tích cho hình chóp đều S.ABCD và có thể tự tin giải các bài toán tương tự. Chúc bạn thành công!