Cho hình chóp đều S.ABC là một dạng bài toán quen thuộc trong chương trình hình học không gian. Để giải quyết các bài toán liên quan đến hình chóp đều S.ABC, ta cần nắm vững các đặc điểm và tính chất của nó. Trong bài viết này, chúng ta sẽ đi sâu vào cách tính chiều cao của hình chóp đều S.ABC, cùng với các ví dụ minh họa và bài tập áp dụng.
Định nghĩa hình chóp đều S.ABC:
Hình chóp đều S.ABC là hình chóp có đáy ABC là tam giác đều và chân đường cao hạ từ đỉnh S xuống mặt phẳng đáy (ABC) trùng với tâm O của tam giác đều ABC.
Các yếu tố cần biết về hình chóp đều S.ABC:
- Đáy (ABC): Tam giác đều cạnh a.
- Đỉnh (S): Điểm nằm ngoài mặt phẳng đáy.
- Đường cao (SH): Đoạn thẳng vuông góc với mặt phẳng đáy, với H là tâm của tam giác đều ABC.
- Mặt bên: Các tam giác SAB, SBC, SCA là các tam giác cân bằng nhau.
- Góc giữa mặt bên và mặt đáy: Góc tạo bởi đường cao của mặt bên và hình chiếu của nó trên mặt đáy.
Bài toán:
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa một mặt bên và mặt đáy bằng 60°. Tính độ dài đường cao SH.
Lời giải:
-
Xác định tâm đáy: Vì S.ABC là hình chóp đều, hình chiếu vuông góc H của S xuống mặt phẳng (ABC) là tâm của tam giác đều ABC.
-
Xác định góc giữa mặt bên và mặt đáy: Gọi M là trung điểm của BC. Góc giữa mặt bên (SBC) và mặt đáy (ABC) là góc SMA. Theo đề bài, góc SMA = 60°.
-
Tính độ dài AM: Trong tam giác đều ABC, AM là đường trung tuyến đồng thời là đường cao. Do đó, AM = (a√3)/2.
-
Tính độ dài HM: Vì H là tâm của tam giác đều ABC, HM = (1/3)AM = (a√3)/6.
-
Tính độ dài SH: Trong tam giác vuông SHM, ta có:
SH = HM tan(SMA) = (a√3)/6 tan(60°) = (a√3)/6 * √3 = a/2.
Vậy, độ dài đường cao SH của hình chóp đều S.ABC là a/2.
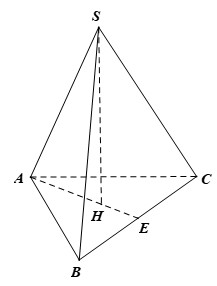{width=217 height=286}Hình chóp đều S.ABC minh họa các yếu tố cơ bản như đỉnh S, đáy ABC, đường cao SH và cạnh đáy a, giúp người học dễ hình dung và nắm bắt bài toán.
Ví dụ khác:
Cho hình chóp đều S.ABC có cạnh đáy bằng 6, góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích hình chóp S.ABC.
Hướng dẫn giải:
- Tính độ dài đường cao SH: Sử dụng tan của góc giữa cạnh bên và mặt đáy, kết hợp với bán kính đường tròn ngoại tiếp tam giác đáy.
- Tính diện tích đáy: Diện tích tam giác đều cạnh 6.
- Tính thể tích: V = (1/3) SH Diện tích đáy.
Hình ảnh minh họa rõ ràng góc SMA giữa mặt bên SBC và mặt đáy ABC, cũng như các đường cao và trung tuyến liên quan, hỗ trợ việc hình dung và giải bài toán hình chóp đều.
Bài tập áp dụng:
- Cho hình chóp đều S.ABC có cạnh đáy bằng 4, đường cao SH = 2√3. Tính góc giữa mặt bên và mặt đáy.
- Cho hình chóp đều S.ABC có thể tích bằng 8√3 và cạnh đáy bằng 4. Tính độ dài đường cao SH.
Kết luận:
Việc nắm vững định nghĩa, tính chất và các công thức liên quan đến hình chóp đều S.ABC là rất quan trọng để giải quyết các bài toán hình học không gian. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn khi đối mặt với các bài toán về hình chóp đều. Hãy luyện tập thêm các bài tập để củng cố kiến thức và nâng cao kỹ năng giải toán.

