Hàm số bậc ba y=ax³+bx²+cx+d là một trong những chủ đề quan trọng trong chương trình Toán học phổ thông và cao cấp. Việc nắm vững kiến thức về hàm số này giúp học sinh, sinh viên giải quyết nhiều bài toán liên quan đến khảo sát hàm số, tìm cực trị, và ứng dụng thực tế. Bài viết này sẽ đi sâu vào các khía cạnh khác nhau của hàm số y=ax³+bx²+cx+d, từ đồ thị đến các tính chất và ứng dụng của nó.
Để hiểu rõ hơn về hàm số bậc ba, chúng ta cần xem xét đồ thị của nó. Dưới đây là một ví dụ về đồ thị của hàm số y=ax³+bx²+cx+d:
Phân tích đồ thị hàm số y=ax³+bx²+cx+d:
- Dạng đồ thị: Đồ thị hàm số bậc ba có thể có nhiều hình dạng khác nhau, tùy thuộc vào giá trị của các hệ số a, b, c, và d.
- Tính đơn điệu: Hàm số có thể đồng biến hoặc nghịch biến trên các khoảng khác nhau.
- Điểm cực trị: Hàm số có thể có hai điểm cực trị (cực đại và cực tiểu), một điểm cực trị hoặc không có điểm cực trị nào.
- Giao điểm với trục tung: Giao điểm của đồ thị với trục tung là điểm (0, d).
Điều kiện để hàm số y=ax³+bx²+cx+d có cực trị:
Để hàm số có cực trị, đạo hàm của nó phải có nghiệm. Ta có:
y' = 3ax² + 2bx + c
Hàm số có cực trị khi và chỉ khi phương trình 3ax² + 2bx + c = 0 có hai nghiệm phân biệt. Điều này tương đương với điều kiện:
Δ' = b² - 3ac > 0
Dấu của các hệ số a, b, c, d:
Dấu của các hệ số a, b, c, d ảnh hưởng trực tiếp đến hình dạng và vị trí của đồ thị hàm số.
- Hệ số a:
- Nếu
a > 0: nhánh cuối của đồ thị hướng lên trên. - Nếu
a < 0: nhánh cuối của đồ thị hướng xuống dưới.
- Nếu
- Hệ số d: Giá trị của d chính là tung độ giao điểm của đồ thị với trục Oy. Nếu d > 0, đồ thị cắt trục Oy tại điểm nằm phía trên trục Ox, và ngược lại.
- Hệ số b và c: Liên quan đến vị trí và tính chất của các điểm cực trị (nếu có).
Ví dụ, xét bài toán sau:
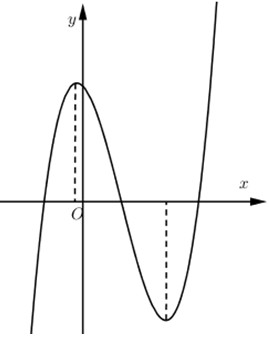
Cho hàm số y=ax³+bx²+cx+d có đồ thị như hình vẽ. Xác định dấu của a, b, c, d.
Phân tích:
- Nhánh cuối đồ thị hướng lên trên =>
a > 0. - Đồ thị cắt trục Oy tại điểm có tung độ dương =>
d > 0. - Hàm số có hai điểm cực trị nằm hai phía trục tung. Điều này cho thấy phương trình
y' = 0có hai nghiệm trái dấu, tức là3ac < 0. Vìa > 0nênc < 0. - Hoành độ trung bình của hai điểm cực trị dương, tức là
x1 + x2 > 0, suy ra-2b/3a > 0. Vìa > 0nênb < 0.
Vậy, ta có: a > 0, b < 0, c < 0, d > 0.
Ứng dụng của hàm số y=ax³+bx²+cx+d:
- Trong toán học: Khảo sát sự biến thiên và vẽ đồ thị hàm số, giải các bài toán liên quan đến cực trị.
- Trong vật lý: Mô tả chuyển động của vật thể, tính toán các đại lượng vật lý.
- Trong kinh tế: Xây dựng các mô hình kinh tế, dự báo xu hướng phát triển.
- Trong kỹ thuật: Thiết kế các hệ thống điều khiển, tối ưu hóa các quy trình sản xuất.
Nắm vững kiến thức về hàm số y=ax³+bx²+cx+d là rất quan trọng để giải quyết các bài toán liên quan và ứng dụng vào thực tế. Việc hiểu rõ đồ thị, tính chất và điều kiện để hàm số có cực trị sẽ giúp bạn tự tin hơn trong học tập và công việc.