Chân Đường Vuông Góc trong Hình Học: Ứng Dụng và Bài Toán Điển Hình

Chân đường Vuông Góc là một khái niệm quan trọng trong hình học, đặc biệt là khi giải các bài toán liên quan đến tam giác, đường tròn và các hình khác. Nó được định nghĩa là giao điểm của một đường thẳng với một đường thẳng khác mà đường thẳng đó vuông góc với đường thẳng ban đầu. Bài viết này sẽ đi sâu vào khái niệm, các ứng dụng và một số bài toán điển hình liên quan đến chân đường vuông góc.

Xét bài toán sau: Cho hình chữ nhật ABCD, gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính độ dài AD, AB (làm tròn đến hàng đơn vị).

Lời giải chi tiết sẽ giúp bạn hiểu rõ hơn về ứng dụng của chân đường vuông góc trong giải toán.

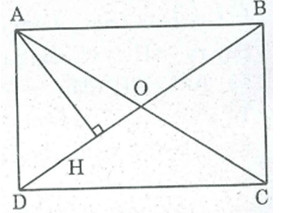Hình chữ nhật ABCD với H là chân đường vuông góc từ A xuống BD

Ta có:

DB = HD + HB = 2 + 6 = 8 (cm)

AC = DB (tính chất hình chữ nhật)

OA = OB = OC = OD = 1/2 BD = 4 (cm)

OD = OH + HD

⇒ OH = OD – HD = 4 – 2 = 2 (cm)

Suy ra: OH = HD = 2 cm nên H là trung điểm của OD

Tam giác ADO có AH là đường cao đồng thời là đường trung tuyến nên tam giác ADO cân tại A

⇒AD = AO = 4 (cm)

Trong tam giác vuông ABD có ∠(BAD) = 900

BD²=AB²+AD² (định lý Pi-ta-go) ⇒ AB²=BD²-AD²

AB = √(BD²-AD²)=√(8²-4²) ≈ 7 (cm).

Các Bài Toán Liên Quan Đến Chân Đường Vuông Góc

Ngoài bài toán trên, có rất nhiều bài toán hình học khác liên quan đến chân đường vuông góc. Dưới đây là một số ví dụ:

1. Tam giác vuông: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là chân đường vuông góc kẻ từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE, với M là trung điểm BC. Bài toán này liên quan đến tính chất đường trung tuyến và chân đường vuông góc trong tam giác vuông.

2. Tam giác cân: Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Xác định hình dạng của tứ giác BEDC. Bài toán này kết hợp tính chất đối xứng và chân đường vuông góc để xác định hình dạng hình học.

3. Ứng dụng trong chứng minh: Trong nhiều bài toán chứng minh, việc xác định và sử dụng chân đường vuông góc giúp đơn giản hóa bài toán và tìm ra lời giải. Ví dụ, chứng minh các đường thẳng đồng quy, các điểm thẳng hàng, hoặc các đoạn thẳng bằng nhau.

Tầm Quan Trọng của Chân Đường Vuông Góc

Chân đường vuông góc không chỉ là một khái niệm hình học đơn thuần mà còn là một công cụ mạnh mẽ trong giải toán. Việc nắm vững khái niệm và các ứng dụng của nó giúp học sinh và người yêu thích toán học dễ dàng tiếp cận và giải quyết các bài toán hình học phức tạp.

Ngoài ra, việc hiểu rõ về chân đường vuông góc còn giúp chúng ta áp dụng vào thực tế, ví dụ như trong thiết kế kỹ thuật, xây dựng, và các lĩnh vực liên quan đến đo đạc và không gian.

Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và sâu sắc về chân đường vuông góc và các ứng dụng của nó. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và kỹ năng giải toán liên quan đến khái niệm này.