Cấp Số Nhân Lùi Vô Hạn là một khái niệm quan trọng trong chương trình Toán 11 và có nhiều ứng dụng thú vị trong thực tế. Bài viết này sẽ cung cấp cho bạn một cái nhìn toàn diện về cấp số nhân lùi vô hạn, từ định nghĩa, công thức tính tổng đến các bài tập vận dụng và mẹo giải nhanh.
1. Định Nghĩa Cấp Số Nhân Lùi Vô Hạn
Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn) trong đó mỗi số hạng, kể từ số hạng thứ hai, đều bằng tích của số hạng đứng ngay trước nó với một số không đổi q, gọi là công bội.
Alt: Dãy số cấp số nhân với các số hạng tăng dần thể hiện mối quan hệ nhân giữa các số
Cấp số nhân $u_n$ được xác định bởi: $u1 = a, u{n+1} = u_n . q (n in N^*)$.
Như vậy, cấp số nhân có dạng: $a, aq, aq^2, aq^3, aq^4,…$ với a là số hạng đầu tiên và q là công bội.
Ví dụ: Cấp số nhân có số hạng đầu là 3, công bội là 2 có dạng: 3, 6, 12, 24, 48,…
Cấp số nhân lùi vô hạn là cấp số nhân có công bội q thỏa mãn điều kiện: $|q| < 1$. Điều này có nghĩa là giá trị tuyệt đối của công bội phải nhỏ hơn 1.
Ví dụ: Các dãy số sau đều là cấp số nhân lùi vô hạn:
- $1; frac{1}{5}; frac{1}{5^2}; …; frac{1}{5^{n-1}}; …$
- $2; -1; frac{1}{2}; -frac{1}{2^2}; …; (-1)^{n-1}frac{1}{2^{n-2}}; …$
- $frac{1}{2}; frac{1}{4}; frac{1}{8}; frac{1}{16}; …$
2. Công Thức Tính Tổng Cấp Số Nhân Lùi Vô Hạn
Điểm đặc biệt của cấp số nhân lùi vô hạn là tổng của tất cả các số hạng của nó hội tụ về một giá trị hữu hạn, có thể tính được bằng công thức.
Cho cấp số nhân lùi vô hạn $u_n$, tổng của các số hạng của nó được tính như sau:
$S = frac{u_1}{1 – q}$
Trong đó:
- S là tổng của cấp số nhân lùi vô hạn
- $u_1$ là số hạng đầu tiên
- q là công bội
Ví dụ 1: Tính tổng của cấp số nhân lùi vô hạn $u_n$ với $u_n = (frac{1}{3})^n$.
Lời giải:
Ta có: $u_1 = frac{1}{3}, q = frac{1}{3}$.
Áp dụng công thức: $S = frac{u_1}{1 – q} = frac{frac{1}{3}}{1 – frac{1}{3}} = frac{1}{2}$.
Ví dụ 2: Cho cấp số nhân lùi vô hạn có số hạng đầu là 4, công bội là $frac{1}{2}$. Tính tổng tất cả các số hạng của cấp số nhân đó.
Lời giải:
Áp dụng công thức: $S = frac{4}{1 – frac{1}{2}} = 8$.
3. Bài Tập Trắc Nghiệm Cấp Số Nhân Lùi Vô Hạn (Có Lời Giải Chi Tiết)
Để giúp bạn nắm vững kiến thức và rèn luyện kỹ năng giải bài tập, dưới đây là một số bài tập trắc nghiệm về cấp số nhân lùi vô hạn, kèm theo lời giải chi tiết:
Câu 1: Cấp số nhân lùi vô hạn sau có tổng các số hạng là bao nhiêu: $frac{1}{2}; -frac{1}{4}; frac{1}{8}; …; frac{(-1)^{n+1}}{2^n}; …$
A. $frac{1}{5}$
B. $frac{1}{7}$
C. $frac{1}{9}$
D. $frac{1}{3}$
Lời giải:
Đây là cấp số nhân lùi vô hạn với $u_1 = frac{1}{2}, q = -frac{1}{2}$.
Tổng $S = frac{u_1}{1 – q} = frac{frac{1}{2}}{1 + frac{1}{2}} = frac{1}{3}$.
Đáp án đúng: D
Câu 2: Cho cấp số nhân lùi vô hạn $u_n = -1; -frac{1}{2}; -frac{1}{4}; -frac{1}{8}; …; (-frac{1}{2})^{n-1}…$. Tính tổng $S_n$.
A. $frac{7}{3}$
B. $frac{1}{3}$
C. $frac{2}{3}$
D. $frac{5}{3}$
Lời giải:
Ta xác định được $u_1 = -1, q = -frac{1}{2}$.
Tổng $S = frac{u_1}{1 – q} = frac{-1}{1 + frac{1}{2}} = -frac{2}{3}$.
Đáp án đúng: Không có đáp án đúng trong các lựa chọn đã cho. Đáp án chính xác là $-frac{2}{3}$.
Câu 3: Tìm số hạng đầu $u_1$ của cấp số nhân lùi vô hạn, biết tổng của cấp số là 3 và công bội là $frac{2}{3}$.
A. 1
B. $left(frac{2}{3}right)^n$
C. $left(frac{2}{3}right)^{n-1}$
D. $left(frac{2}{3}right)^{n+1}$
Lời giải:
$S = frac{u_1}{1 – q} = frac{u_1}{1 – frac{2}{3}} = 3 Rightarrow u_1 = 1$
Đáp án đúng: A
Câu 4: Tính tổng của dãy số sau: $-1 + frac{1}{10} – frac{1}{10^2} + frac{1}{10^3} … frac{(-1)^n}{10^{n-1}}…$
A. $frac{1}{11}$
B. $frac{5}{11}$
C. $frac{8}{11}$
D. $-frac{10}{11}$
Lời giải:
$un = frac{(-1)^n}{10^{n-1}}; u{n+1} = frac{(-1)^{n+1}}{10^n} Rightarrow u_{n+1} = -frac{1}{10}u_n$
Tổng các số lập thành một cấp số nhân lùi vô hạn với $u_1 = -1, q = -frac{1}{10}$
=> $S = frac{u_1}{1 – q} = frac{-1}{1 + frac{1}{10}} = -frac{10}{11}$
Đáp án đúng: D
Alt: Hình ảnh minh họa cách giải bài toán cấp số nhân lùi vô hạn bằng phương pháp đại số
Câu 5: Tổng của một cấp số nhân lùi vô hạn là $frac{5}{3}$, tổng của ba số hạng đầu là $frac{39}{25}$. Tìm số hạng đầu $u_1$ và công bội q của cấp số đó.
A. $u_1 = 1, q = frac{2}{5}$
B. $u_1 = 1, q = -frac{2}{5}$
C. $u_1 = -1, q = frac{2}{5}$
D. $u_1 = -1, q = -frac{2}{5}$
Lời giải:
$left{begin{matrix} S = frac{u_1}{1 – q} = frac{5}{3} \ u_1 + u_1q + u_1q^2 = frac{39}{25} end{matrix}right.$
$Rightarrow left{begin{matrix} u_1 = frac{5}{3}(1 – q) \ u_1(1 + q + q^2) = frac{39}{25} end{matrix}right.$
Thay $u_1$ từ phương trình 1 vào phương trình 2:
$frac{5}{3}(1 – q)(1 + q + q^2) = frac{39}{25}$
$frac{5}{3}(1 – q^3) = frac{39}{25}$
$1 – q^3 = frac{39}{25} * frac{3}{5} = frac{117}{125}$
$q^3 = 1 – frac{117}{125} = frac{8}{125}$
$q = sqrt[3]{frac{8}{125}} = frac{2}{5}$
Thay q vào phương trình 1:
$u_1 = frac{5}{3}(1 – frac{2}{5}) = frac{5}{3} * frac{3}{5} = 1$
Đáp án đúng: A
Các câu còn lại bạn có thể tự giải tương tự để luyện tập thêm.
4. Ứng Dụng Của Cấp Số Nhân Lùi Vô Hạn
Cấp số nhân lùi vô hạn không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng thực tế, ví dụ như:
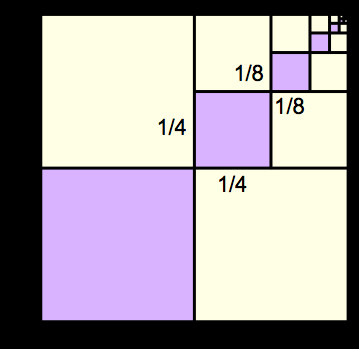
- Tính diện tích và thể tích: Trong hình học, cấp số nhân lùi vô hạn được sử dụng để tính diện tích của các hình fractal hoặc thể tích của các vật thể có cấu trúc phức tạp.
- Kinh tế: Mô hình hóa sự tăng trưởng hoặc suy giảm kinh tế theo thời gian.
- Vật lý: Mô tả sự phân rã của các chất phóng xạ hoặc dao động tắt dần.
- Khoa học máy tính: Phân tích hiệu suất của các thuật toán đệ quy.
5. Mẹo Giải Nhanh Bài Tập Cấp Số Nhân Lùi Vô Hạn
- Xác định đúng công bội: Đây là bước quan trọng nhất. Hãy chắc chắn rằng bạn đã tính toán chính xác giá trị của q.
- Kiểm tra điều kiện |q| < 1: Nếu điều kiện này không được thỏa mãn, bạn không thể sử dụng công thức tính tổng cấp số nhân lùi vô hạn.
- Sử dụng máy tính cầm tay: Để tính toán nhanh các phép tính phức tạp.
Hy vọng với bài viết này, bạn đã có cái nhìn tổng quan và sâu sắc về cấp số nhân lùi vô hạn. Chúc bạn học tốt và đạt kết quả cao trong các kỳ thi!