Tam giác vuông là một hình học quen thuộc, và việc chứng minh sự bằng nhau giữa các tam giác vuông là một kỹ năng quan trọng. Trong số các trường hợp bằng nhau, trường hợp Cạnh Huyền Góc Nhọn đóng vai trò then chốt. Bài viết này sẽ đi sâu vào trường hợp này, cung cấp kiến thức đầy đủ và các dạng bài tập thường gặp.
1. Định Nghĩa và Tính Chất Của Tam Giác Vuông
Trước khi đi vào chi tiết về trường hợp bằng nhau cạnh huyền góc nhọn, chúng ta cần nắm vững định nghĩa và các tính chất cơ bản của tam giác vuông:
- Định nghĩa: Tam giác vuông là tam giác có một góc bằng 90 độ.
- Các cạnh:
- Cạnh huyền: Cạnh đối diện với góc vuông (cạnh lớn nhất).
- Cạnh góc vuông: Hai cạnh còn lại tạo thành góc vuông.
2. Trường Hợp Bằng Nhau: Cạnh Huyền Góc Nhọn
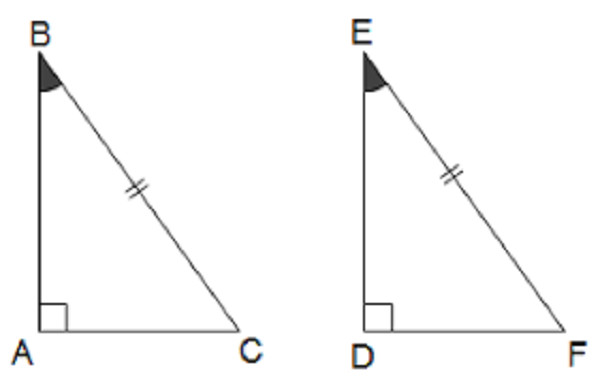
Hai tam giác vuông được gọi là bằng nhau nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia.
Hai tam giác vuông bằng nhau khi cạnh huyền và góc nhọn tương ứng bằng nhau, minh họa định lý cạnh huyền góc nhọn.
3. Chứng Minh Trường Hợp Bằng Nhau Cạnh Huyền Góc Nhọn
Giả sử ta có hai tam giác vuông ABC (góc A = 90°) và DEF (góc D = 90°), với BC = EF (cạnh huyền) và góc C = góc F (góc nhọn). Để chứng minh ΔABC = ΔDEF, ta thực hiện như sau:
- Xét tổng góc trong tam giác: Vì góc A = góc D = 90°, nên góc B = 90° – góc C và góc E = 90° – góc F. Do góc C = góc F, suy ra góc B = góc E.
- Áp dụng trường hợp góc-cạnh-góc: Ta có góc C = góc F (giả thiết), BC = EF (giả thiết), và góc B = góc E (chứng minh trên). Vậy, ΔABC = ΔDEF (góc-cạnh-góc).
4. Các Dạng Bài Tập Về Cạnh Huyền Góc Nhọn
4.1. Chứng minh hai tam giác vuông bằng nhau
Đây là dạng bài tập cơ bản, yêu cầu học sinh xác định yếu tố cạnh huyền góc nhọn và áp dụng định lý để chứng minh.
4.2. Tính toán các yếu tố trong tam giác
Dạng bài này kết hợp việc chứng minh tam giác bằng nhau với việc tính toán độ dài cạnh, số đo góc. Sau khi chứng minh hai tam giác bằng nhau nhờ trường hợp cạnh huyền góc nhọn, ta có thể suy ra các yếu tố tương ứng bằng nhau.
4.3. Bài toán thực tế
Các bài toán thực tế thường liên quan đến việc ứng dụng kiến thức tam giác vuông để giải quyết các vấn đề đo đạc, thiết kế.
5. Ví Dụ Minh Họa
Ví dụ: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC tại D. Kẻ DH vuông góc với BC tại H. Chứng minh rằng:
a) Tam giác ABD = tam giác HBD
b) BD là đường trung trực của đoạn AH
Giải:
a) Xét ΔABD và ΔHBD có:
- Góc A = Góc H = 90°
- BD là cạnh chung
- Góc ABD = Góc HBD (do BD là tia phân giác của góc B)
Hình minh họa hai tam giác vuông ABD và HBD có cạnh huyền và góc nhọn bằng nhau.
Vậy, ΔABD = ΔHBD (cạnh huyền – góc nhọn).
b) Vì ΔABD = ΔHBD (chứng minh trên), suy ra AD = HD (hai cạnh tương ứng). Do đó, D nằm trên đường trung trực của đoạn AH. Mặt khác, BD là đường phân giác của góc ABH nên BD cũng là đường trung trực của AH. Vậy BD là đường trung trực của đoạn AH.
6. Lưu Ý Khi Giải Bài Tập
- Vẽ hình chính xác: Một hình vẽ rõ ràng sẽ giúp bạn dễ dàng nhận ra các yếu tố cần thiết.
- Xác định đúng yếu tố: Kiểm tra kỹ các yếu tố cạnh huyền và góc nhọn để đảm bảo chúng tương ứng và bằng nhau.
- Trình bày logic: Viết các bước chứng minh một cách rõ ràng, sử dụng các ký hiệu toán học chính xác.
Nắm vững lý thuyết và luyện tập thường xuyên là chìa khóa để thành thạo các bài toán liên quan đến trường hợp bằng nhau cạnh huyền góc nhọn của tam giác vuông. Chúc các bạn học tốt!