Đường tròn nội tiếp tam giác là một khái niệm quan trọng trong hình học phẳng. Nắm vững cách xác định tâm và bán kính của đường tròn này sẽ giúp bạn giải quyết nhiều bài toán liên quan đến tam giác. Bài viết này sẽ hướng dẫn chi tiết Cách Vẽ Tâm đường Tròn Nội Tiếp Tam Giác, kèm theo các ví dụ và bài tập minh họa.
Định Nghĩa Đường Tròn Nội Tiếp Tam Giác
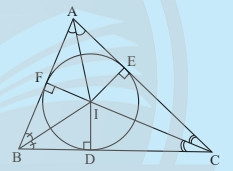
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác đó. Tâm của đường tròn nội tiếp là điểm đồng quy của ba đường phân giác trong của tam giác.
Cách Xác Định Tâm Đường Tròn Nội Tiếp Tam Giác
Để vẽ tâm đường tròn nội tiếp tam giác, ta thực hiện các bước sau:
-
Vẽ tam giác: Cho tam giác ABC bất kỳ.
-
Vẽ các đường phân giác: Sử dụng thước và compa để vẽ hai đường phân giác trong của hai góc bất kỳ của tam giác (ví dụ, góc A và góc B).
-
Xác định giao điểm: Giao điểm của hai đường phân giác này chính là tâm I của đường tròn nội tiếp tam giác ABC.
Ảnh minh họa: Tâm I của đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác.
Cách Vẽ Đường Tròn Nội Tiếp Tam Giác
Sau khi xác định được tâm I, ta thực hiện các bước sau để vẽ đường tròn:
-
Dựng đường vuông góc: Từ tâm I, vẽ một đường vuông góc xuống một cạnh bất kỳ của tam giác (ví dụ, cạnh BC). Gọi H là chân đường vuông góc.
-
Xác định bán kính: Độ dài đoạn IH chính là bán kính r của đường tròn nội tiếp.
-
Vẽ đường tròn: Vẽ đường tròn tâm I bán kính r. Đường tròn này chính là đường tròn nội tiếp tam giác ABC.
Đường Tròn Nội Tiếp Tam Giác Đều
Trong trường hợp tam giác đều, tâm đường tròn nội tiếp trùng với trọng tâm, trực tâm và tâm đường tròn ngoại tiếp của tam giác. Bán kính r của đường tròn nội tiếp tam giác đều cạnh a được tính theo công thức:
Hình ảnh minh họa: Vị trí tương quan giữa đường tròn nội tiếp và ngoại tiếp trong tam giác đều.
Bài Tập Vận Dụng
Để củng cố kiến thức, chúng ta cùng xét một số bài tập vận dụng:
Bài 1: Cho tam giác ABC có AB = 6cm, BC = 8cm, CA = 10cm. Chứng minh rằng tam giác ABC vuông tại B. Tính bán kính đường tròn nội tiếp tam giác ABC.
Hướng dẫn:
- Sử dụng định lý Pythagore đảo để chứng minh tam giác ABC vuông tại B.
- Áp dụng công thức tính diện tích tam giác vuông: S = (AB * BC) / 2.
- Tính nửa chu vi tam giác: p = (AB + BC + CA) / 2.
- Áp dụng công thức tính bán kính đường tròn nội tiếp: r = S / p.
Bài 2: Cho tam giác đều ABC cạnh a. Tính bán kính đường tròn nội tiếp tam giác ABC theo a.
Hướng dẫn:
- Sử dụng công thức tính bán kính đường tròn nội tiếp tam giác đều:
Hình ảnh minh họa cách vẽ đường tròn nội tiếp tam giác ABC bằng thước và compa.
Ứng Dụng Thực Tế
Việc nắm vững cách vẽ và tính toán các yếu tố liên quan đến đường tròn nội tiếp tam giác không chỉ hữu ích trong học tập mà còn có ứng dụng trong thực tế, ví dụ như trong thiết kế, kiến trúc, và các bài toán liên quan đến tối ưu hóa khoảng cách.
Kết Luận
Hi vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức về cách vẽ tâm đường tròn nội tiếp tam giác. Hãy luyện tập thường xuyên để nắm vững kỹ năng này và áp dụng vào giải các bài toán hình học một cách hiệu quả. Chúc các bạn học tốt!