Phương trình mũ là một phần quan trọng trong chương trình toán học phổ thông và thường xuyên xuất hiện trong các kỳ thi. Việc nắm vững các phương pháp Cách Tính Tập Nghiệm Của Phương Trình mũ là vô cùng cần thiết. Bài viết này sẽ cung cấp một cái nhìn toàn diện về vấn đề này, từ lý thuyết cơ bản đến các phương pháp giải toán hiệu quả, cùng với các ví dụ minh họa và bài tập áp dụng.
1. Tổng Quan Về Phương Trình Mũ
Phương trình mũ là phương trình trong đó ẩn số xuất hiện ở số mũ. Dạng tổng quát của phương trình mũ là:
trong đó:
- a là cơ số, a > 0 và a ≠ 1
- x là ẩn số
- b là một số thực
Để giải phương trình mũ, mục tiêu là tìm tất cả các giá trị của x thỏa mãn phương trình. Cách tính tập nghiệm của phương trình này phụ thuộc vào dạng của phương trình và các kỹ thuật biến đổi.
2. Các Phương Pháp Cơ Bản Để Tìm Tập Nghiệm
2.1. Đưa Về Cùng Cơ Số
Đây là phương pháp phổ biến nhất và thường được áp dụng cho các phương trình mũ đơn giản. Ý tưởng chính là biến đổi phương trình sao cho cả hai vế có cùng cơ số. Khi đó, ta có thể so sánh số mũ.
Ví dụ: Giải phương trình
Giải:
Ta có thể viết lại phương trình như sau:
Vì cơ số 3 > 1, ta có thể so sánh số mũ:
Giải bất phương trình bậc hai này, ta được -1 < x < 2.
Vậy tập nghiệm của bất phương trình mũ là (-1; 2).
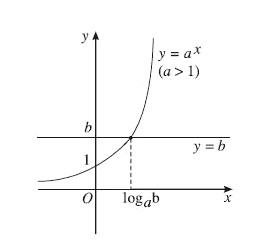
Alt text: Đồ thị hàm số y = a^x với a > 1, minh họa tính đồng biến của hàm số mũ, hỗ trợ cách tính tập nghiệm.
2.2. Đặt Ẩn Phụ
Phương pháp này được sử dụng khi phương trình mũ có dạng phức tạp hơn, chứa các biểu thức mũ lặp lại. Bằng cách đặt một ẩn phụ, ta có thể đưa phương trình về dạng đơn giản hơn, dễ giải hơn.
Ví dụ: Giải phương trình
Alt text: Ví dụ minh họa phương trình mũ phức tạp cần đặt ẩn phụ để đơn giản hóa quá trình tìm tập nghiệm.
2.3. Logarit Hóa
Khi không thể đưa về cùng cơ số, ta có thể sử dụng logarit để giải phương trình mũ. Lấy logarit cả hai vế của phương trình sẽ giúp đưa ẩn số từ số mũ xuống.
Ví dụ: Giải phương trình
Alt text: Công thức logarit hóa phương trình mũ để đưa về dạng dễ giải, phương pháp quan trọng trong cách tính tập nghiệm.
2.4. Sử Dụng Tính Đơn Điệu Của Hàm Số
Nếu một vế của phương trình là hàm đồng biến và vế còn lại là hàm nghịch biến (hoặc là một hằng số), ta có thể sử dụng tính đơn điệu để xác định nghiệm của phương trình.
Ví dụ: Giải phương trình
Alt text: Áp dụng tính đơn điệu của hàm số để tìm tập nghiệm cho phương trình mũ khi các phương pháp khác khó áp dụng.
3. Các Dạng Bài Tập Thường Gặp Và Cách Giải
- Phương trình mũ cơ bản: Áp dụng phương pháp đưa về cùng cơ số hoặc logarit hóa.
- Phương trình mũ chứa tham số: Tìm điều kiện của tham số để phương trình có nghiệm hoặc có nghiệm thỏa mãn điều kiện cho trước.
- Hệ phương trình mũ: Kết hợp các phương pháp trên để giải từng phương trình trong hệ, sau đó tìm nghiệm chung.
4. Lưu Ý Khi Giải Phương Trình Mũ
- Luôn kiểm tra điều kiện của cơ số (a > 0 và a ≠ 1).
- Khi đặt ẩn phụ, cần tìm điều kiện cho ẩn phụ để đảm bảo nghiệm tìm được là hợp lệ.
- Khi logarit hóa, cần chú ý đến điều kiện của biểu thức trong logarit (lớn hơn 0).
- Kiểm tra lại nghiệm sau khi giải để đảm bảo nghiệm thỏa mãn phương trình ban đầu.
5. Bài Tập Áp Dụng
Dưới đây là một số bài tập áp dụng để bạn luyện tập cách tính tập nghiệm của phương trình mũ:
- Giải phương trình: 2^(x+1) = 8
- Giải phương trình: 3^(2x) – 4 * 3^x + 3 = 0
- Giải bất phương trình: (1/2)^x > 4
6. Kết Luận
Nắm vững lý thuyết và luyện tập thường xuyên các phương pháp giải phương trình mũ là chìa khóa để thành công trong các bài kiểm tra và kỳ thi. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về cách tính tập nghiệm của phương trình mũ. Chúc bạn học tốt!