Bài viết này sẽ cung cấp một hướng dẫn toàn diện về cách xác định và tính toán phản lực liên kết, một khái niệm quan trọng trong cơ học lý thuyết. Chúng ta sẽ khám phá các khái niệm cơ bản, các loại liên kết phổ biến và quy trình từng bước để giải quyết các bài toán liên quan đến phản lực liên kết.
1. Khái Niệm Cơ Bản Về Phản Lực Liên Kết
Trước khi đi sâu vào Cách Tính Phản Lực Liên Kết, chúng ta cần nắm vững một số định nghĩa và khái niệm cơ bản:
-
Lực: Là đại lượng vectơ biểu thị tác dụng cơ học giữa các vật, có xu hướng làm thay đổi trạng thái chuyển động hoặc gây biến dạng cho vật. Lực được đặc trưng bởi điểm đặt, phương, chiều và độ lớn (đơn vị: Newton – N).
-
Mô men lực: Đại lượng vật lý thể hiện khả năng gây ra chuyển động quay của vật quanh một trục hoặc một điểm. Mô men lực phụ thuộc vào độ lớn của lực và khoảng cách từ trục quay đến đường tác dụng của lực (cánh tay đòn). Công thức tính mô men lực: M = F * d (đơn vị: N.m).
-
Cơ hệ: Tập hợp các chất điểm hoặc vật thể có liên quan với nhau về mặt cơ học.
-
Hệ lực: Tập hợp các lực tác dụng lên một cơ hệ hoặc vật thể.
-
Hệ lực cân bằng: Hệ lực mà tổng hợp của tất cả các lực và mô men lực bằng không. Hệ lực cân bằng không gây ra bất kỳ tác dụng cơ học nào lên cơ hệ.
2. Các Loại Liên Kết Thường Gặp và Phản Lực Tương Ứng
Trong cơ học, liên kết là các ràng buộc hạn chế chuyển động của vật thể. Mỗi loại liên kết sẽ tạo ra một hoặc nhiều phản lực để chống lại sự chuyển động bị hạn chế. Dưới đây là các loại liên kết phổ biến và các phản lực liên kết tương ứng:
-
Liên kết cố định (Gối cố định): Liên kết này ngăn chặn cả chuyển động tịnh tiến theo hai phương (x và y). Do đó, gối cố định tạo ra hai phản lực liên kết, thường được ký hiệu là H (phản lực theo phương ngang) và V (phản lực theo phương thẳng đứng).
-
Liên kết di động (Gối di động): Liên kết này cho phép vật thể chuyển động theo một phương (thường là phương ngang) nhưng ngăn chặn chuyển động theo phương vuông góc với phương trượt. Do đó, gối di động tạo ra một phản lực liên kết, thường được ký hiệu là V, theo phương vuông góc với phương trượt.
-
Liên kết ngàm: Đây là loại liên kết mạnh nhất, ngăn chặn cả chuyển động tịnh tiến theo hai phương (x và y) và chuyển động quay. Do đó, liên kết ngàm tạo ra hai phản lực liên kết (H và V) và một mô men phản lực (M) để chống lại sự quay.
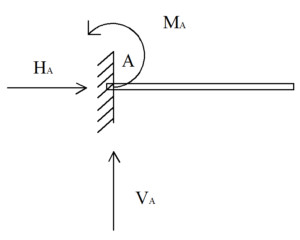Phản lực liên kết tại ngàm gồm hai thành phần lực H, V và một mô men M
3. Quy Trình Tính Phản Lực Liên Kết
Để tính phản lực liên kết, chúng ta thường thực hiện theo các bước sau:
Bước 1: Xác định và ký hiệu các phản lực liên kết lên sơ đồ vật thể tự do (FBD).
- Vẽ sơ đồ vật thể tự do (FBD) của vật thể hoặc cơ hệ cần xét.
- Xác định các loại liên kết và ký hiệu các phản lực liên kết tương ứng tại mỗi liên kết. Chọn chiều dương cho các phản lực liên kết một cách tùy ý. Nếu kết quả tính toán là âm, điều đó có nghĩa là chiều của phản lực liên kết ngược lại với chiều đã chọn ban đầu.
Bước 2: Phân tích các lực tác dụng lên vật thể.
- Liệt kê tất cả các lực tác dụng lên vật thể, bao gồm cả lực tác dụng trực tiếp (ví dụ: trọng lực, lực kéo, lực đẩy) và các phản lực liên kết.
- Đối với các lực phân bố, thay thế chúng bằng lực tương đương tác dụng tại trọng tâm của vùng phân bố. Ví dụ, đối với lực phân bố đều q, lực tương đương sẽ là Q = q * L (với L là chiều dài vùng phân bố) và tác dụng tại trung điểm của vùng phân bố.
Bước 3: Áp dụng các phương trình cân bằng tĩnh học.
- Trong cơ học tĩnh học, một vật thể ở trạng thái cân bằng khi tổng tất cả các lực và mô men lực tác dụng lên nó bằng không. Điều này dẫn đến các phương trình cân bằng sau:
- Tổng các lực theo phương x bằng 0: ∑Fx = 0
- Tổng các lực theo phương y bằng 0: ∑Fy = 0
- Tổng các mô men lực đối với một điểm bất kỳ bằng 0: ∑M = 0
- Chọn một hệ tọa độ phù hợp (ví dụ: hệ tọa độ Descartes Oxy) và viết các phương trình cân bằng dựa trên các lực và mô men lực đã được xác định ở bước 2.
Bước 4: Giải hệ phương trình và xác định các phản lực liên kết.
- Giải hệ phương trình cân bằng để tìm ra các giá trị của các phản lực liên kết.
- Nếu một phản lực liên kết có giá trị âm, điều đó có nghĩa là chiều thực tế của phản lực liên kết ngược lại với chiều đã chọn ban đầu.
Bước 5: Kiểm tra lại kết quả.
- Sau khi tính toán xong, hãy kiểm tra lại kết quả bằng cách thay các giá trị phản lực liên kết vào các phương trình cân bằng để đảm bảo rằng chúng được thỏa mãn.
4. Ví Dụ Minh Họa
Để hiểu rõ hơn về quy trình tính phản lực liên kết, chúng ta sẽ xem xét một vài ví dụ cụ thể.
Ví dụ 1:
Một dầm AB có chiều dài L = 4m chịu tác dụng của một lực tập trung P = 10kN tại điểm C cách A một khoảng AC = 1m và một mô men M = 5kN.m tác dụng tại điểm B. Dầm được đỡ bởi một gối cố định tại A và một gối di động tại B. Hãy xác định các phản lực liên kết tại A và B.
Giải:
- Bước 1: Vẽ FBD và ký hiệu các phản lực liên kết. Tại A có hai phản lực là HA và VA, tại B có một phản lực là VB.
- Bước 2: Phân tích các lực tác dụng. Chúng ta có lực P, mô men M và các phản lực HA, VA, VB.
- Bước 3: Áp dụng các phương trình cân bằng:
- ∑Fx = HA = 0
- ∑Fy = VA + VB – P = 0
- ∑MA = VB L – P AC – M = 0
- Bước 4: Giải hệ phương trình:
- Từ phương trình đầu tiên, ta có HA = 0.
- Từ phương trình thứ ba, ta có VB = (P AC + M) / L = (10 1 + 5) / 4 = 3.75 kN.
- Thay VB vào phương trình thứ hai, ta có VA = P – VB = 10 – 3.75 = 6.25 kN.
- Bước 5: Kiểm tra lại kết quả. Thay các giá trị HA, VA, VB vào các phương trình cân bằng, ta thấy chúng được thỏa mãn.
Vậy, các phản lực liên kết là HA = 0, VA = 6.25 kN và VB = 3.75 kN.
Ví dụ 2:
Một thanh AB dài 3m được gắn ngàm tại A và chịu tác dụng của một lực phân bố đều q = 2kN/m trên toàn bộ chiều dài. Xác định các phản lực liên kết tại ngàm A.
Giải:
- Bước 1: Vẽ FBD và ký hiệu các phản lực liên kết. Tại A có hai phản lực là HA và VA, và một mô men phản lực là MA.
- Bước 2: Phân tích các lực tác dụng. Chúng ta có lực phân bố đều q và các phản lực HA, VA, MA. Thay lực phân bố đều bằng lực tương đương Q = q L = 2 3 = 6 kN tác dụng tại trung điểm của AB.
- Bước 3: Áp dụng các phương trình cân bằng:
- ∑Fx = HA = 0
- ∑Fy = VA – Q = 0
- ∑MA = MA – Q * (L/2) = 0
- Bước 4: Giải hệ phương trình:
- Từ phương trình đầu tiên, ta có HA = 0.
- Từ phương trình thứ hai, ta có VA = Q = 6 kN.
- Từ phương trình thứ ba, ta có MA = Q (L/2) = 6 (3/2) = 9 kN.m.
Vậy, các phản lực liên kết là HA = 0, VA = 6 kN và MA = 9 kN.m.
5. Ứng Dụng Của Việc Tính Phản Lực Liên Kết
Việc tính toán phản lực liên kết là một bước quan trọng trong việc phân tích kết cấu và thiết kế các công trình xây dựng, máy móc và các hệ thống cơ khí khác. Bằng cách xác định các phản lực liên kết, chúng ta có thể:
- Đánh giá sự ổn định và khả năng chịu tải của kết cấu.
- Xác định nội lực (lực cắt, mô men uốn) trong các thành phần kết cấu.
- Thiết kế các thành phần kết cấu sao cho chúng có đủ độ bền và độ cứng để chịu được các tải trọng tác dụng.
Kết luận
Bài viết này đã cung cấp một hướng dẫn chi tiết về cách tính phản lực liên kết, từ các khái niệm cơ bản đến quy trình giải quyết bài toán và các ví dụ minh họa. Hy vọng rằng, với những kiến thức này, bạn có thể tự tin giải quyết các bài toán liên quan đến phản lực liên kết trong cơ học. Chúc bạn thành công!
