Cách Tính Logarit Bằng Máy Tính Nhanh Chóng và Hiệu Quả

Để giải quyết các bài toán logarit một cách nhanh chóng và chính xác, việc sử dụng máy tính là vô cùng quan trọng. Bài viết này sẽ hướng dẫn chi tiết các phương pháp Cách Tính Logarit Bằng Máy Tính, giúp bạn vượt qua các bài kiểm tra và kỳ thi một cách dễ dàng.

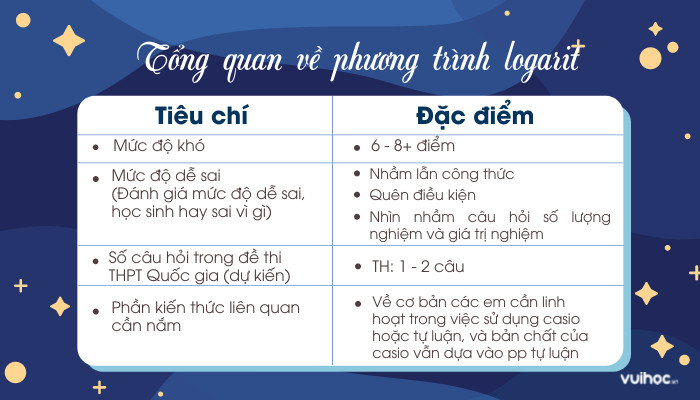
Hình ảnh minh họa tổng quan kiến thức về phương trình logarit và các kỹ năng cần thiết để giải quyết bài toán.

1. Tổng Quan Về Logarit

1.1. Định Nghĩa

Logarit của một số là số mũ mà cơ số phải được nâng lên để tạo ra số đó. Nó là phép toán nghịch đảo của lũy thừa. Công thức tổng quát:

logₐ(b) = x  ⇔  aˣ = b

Trong đó:

• a là cơ số (a > 0, a ≠ 1)
• b là số cần tính logarit (b > 0)
• x là logarit của b theo cơ số a

1.2. Các Loại Logarit Thường Gặp

• Logarit thập phân (log): Cơ số là 10, ký hiệu là log₁₀(b) hoặc log(b).
• Logarit tự nhiên (ln): Cơ số là số e (≈ 2.71828), ký hiệu là ln(b) hoặc logₑ(b).
• Logarit cơ số bất kỳ: Có thể tính được nhờ công thức đổi cơ số (sẽ được đề cập bên dưới).

2. Các Phương Pháp Tính Logarit Bằng Máy Tính

2.1. Sử Dụng Chức Năng Logarit Cơ Bản

Hầu hết các máy tính khoa học đều có sẵn các phím chức năng log (logarit thập phân) và ln (logarit tự nhiên).

Ví dụ:

• Tính log(100): Nhập log(100) và bấm “=”, kết quả sẽ là 2.
• Tính ln(e): Nhập ln(e) (hoặc ln(2.71828)) và bấm “=”, kết quả sẽ xấp xỉ 1.

2.2. Sử Dụng Công Thức Đổi Cơ Số

Để tính logarit với cơ số bất kỳ (ví dụ: log₂(8)), bạn cần sử dụng công thức đổi cơ số:

logₐ(b) = logₓ(b) / logₓ(a)

Trong đó x là một cơ số tùy ý, thường là 10 hoặc e (vì máy tính có sẵn các hàm log và ln).

Ví dụ: Tính log₂(8)

1. Chọn cơ số 10 (log): log₂(8) = log(8) / log(2)
2. Chọn cơ số e (ln): log₂(8) = ln(8) / ln(2)

Trên máy tính, bạn thực hiện như sau:

• log(8) / log(2) hoặc ln(8) / ln(2) rồi bấm “=”, kết quả sẽ là 3.

Ảnh minh họa các công thức biến đổi logarit quan trọng, hỗ trợ việc tính toán và giải quyết các bài toán phức tạp.

2.3. Giải Phương Trình Logarit Bằng Máy Tính Casio FX-570VN PLUS

Máy tính Casio FX-570VN PLUS và các dòng tương tự có nhiều tính năng hỗ trợ giải phương trình logarit:

• CALC (Solve): Cho phép bạn thay các giá trị vào phương trình và kiểm tra. Thích hợp cho các bài trắc nghiệm.
• SHIFT + CALC (Solve): Giải phương trình tìm nghiệm trực tiếp. Tuy nhiên, cần lưu ý tính năng này có thể không tìm được tất cả các nghiệm hoặc đưa ra kết quả gần đúng.
• TABLE (Mode 7): Tạo bảng giá trị để dò nghiệm gần đúng.

2.3.1. Giải Phương Trình Logarit Bằng CALC

Bước 1: Chuyển phương trình về dạng f(x) = 0.
Bước 2: Nhập biểu thức f(x) vào máy tính.
Bước 3: Sử dụng phím CALC để thay các giá trị từ các đáp án trắc nghiệm vào x.
Bước 4: Nếu f(x) = 0, giá trị đó là nghiệm của phương trình.

Ví dụ: Giải phương trình log₂(x) + log₄(x) = 3

Bước 1: Chuyển về dạng: log₂(x) + log₄(x) – 3 = 0

Bước 2: Nhập vào máy tính: log₂(x) + log₄(x) - 3 (Lưu ý: log₄(x) = log(x)/log(4) hoặc ln(x)/ln(4))

Bước 3: Bấm CALC và nhập các giá trị x từ các đáp án.

2.3.2. Giải Phương Trình Logarit Bằng SHIFT + CALC (SOLVE)

Bước 1: Chuyển phương trình về dạng f(x) = 0.
Bước 2: Nhập biểu thức f(x) vào máy tính.
Bước 3: Bấm SHIFT + CALC. Máy tính sẽ hỏi giá trị khởi tạo cho x (bạn có thể nhập một giá trị bất kỳ).
Bước 4: Máy tính sẽ hiển thị nghiệm gần đúng của phương trình.

Lưu ý: Phương pháp này có thể không tìm được tất cả các nghiệm hoặc cho kết quả không chính xác trong một số trường hợp.

2.3.3. Giải Phương Trình Logarit Bằng TABLE (MODE 7)

Bước 1: Chuyển phương trình về dạng f(x) = 0.
Bước 2: Nhập hàm số f(x) vào máy tính bằng cách vào MODE -> 7 (TABLE).
Bước 3: Chọn khoảng giá trị cho x (Start, End, Step).
Bước 4: Quan sát bảng giá trị. Nghiệm của phương trình là giá trị x mà tại đó f(x) đổi dấu hoặc f(x) gần bằng 0.

Ảnh minh họa các công thức biến đổi phương trình logarit, giúp đơn giản hóa bài toán và tìm ra hướng giải quyết.

Ví dụ: Giải phương trình log₂(x-1) = 3 – x

1. Bước 1: Chuyển về dạng f(x) = log₂(x-1) + x – 3 = 0
2. Bước 2: Vào MODE -> 7 và nhập hàm f(x) = log₂(x-1) + x – 3
3. Bước 3: Chọn Start = 2, End = 5, Step = 0.5
4. Bước 4: Quan sát bảng giá trị, ta thấy f(x) đổi dấu giữa x = 2.5 và x = 3. Vậy nghiệm nằm trong khoảng này. Tiếp tục thu hẹp khoảng giá trị để tìm nghiệm chính xác hơn.

3. Lưu Ý Khi Sử Dụng Máy Tính Để Tính Logarit

• Kiểm tra cơ số: Đảm bảo bạn đã nhập đúng cơ số khi sử dụng công thức đổi cơ số.
• Miền xác định: Luôn kiểm tra điều kiện xác định của logarit (b > 0) trước khi tính toán.
• Sai số: Các phương pháp giải phương trình bằng máy tính có thể cho kết quả gần đúng, đặc biệt là với các phương trình phức tạp.
• Luyện tập: Thực hành giải nhiều bài tập khác nhau để làm quen với các thao tác trên máy tính và các phương pháp giải toán logarit.

4. Kết Luận

Nắm vững cách tính logarit bằng máy tính là một kỹ năng quan trọng giúp bạn giải quyết các bài toán liên quan đến logarit một cách nhanh chóng và chính xác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để chinh phục các bài toán logarit trong học tập và thi cử.