Tiệm cận ngang là một khái niệm quan trọng trong chương trình giải tích, đặc biệt khi xét đến đồ thị hàm số. Bài viết này sẽ cung cấp một cái nhìn toàn diện về Cách Tìm Tiệm Cận Ngang, từ định nghĩa cơ bản đến các phương pháp giải bài tập nâng cao, giúp bạn tự tin chinh phục mọi dạng toán liên quan.
1. Định Nghĩa Tiệm Cận Ngang
Tiệm cận ngang của đồ thị hàm số y = f(x) là đường thẳng y = b mà đồ thị hàm số tiến gần đến khi x tiến tới vô cực (cả dương vô cực và âm vô cực).
Nói cách khác:
- Nếu $lim_{xrightarrow +infty } f(x) = b$, thì y = b là tiệm cận ngang của đồ thị hàm số khi x tiến tới dương vô cực.
- Nếu $lim_{xrightarrow -infty } f(x) = b$, thì y = b là tiệm cận ngang của đồ thị hàm số khi x tiến tới âm vô cực.
Một hàm số có thể có tối đa hai đường tiệm cận ngang (một khi x tiến tới dương vô cực và một khi x tiến tới âm vô cực) hoặc không có đường tiệm cận ngang nào.
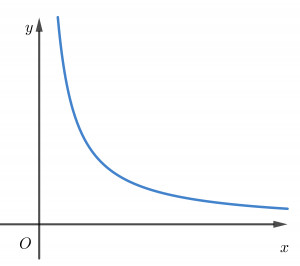
Ảnh: Minh họa đồ thị hàm số với đường tiệm cận ngang, thể hiện sự tiến gần của đồ thị khi x tiến đến vô cực.
2. Phương Pháp Tìm Tiệm Cận Ngang
Để tìm tiệm cận ngang của đồ thị hàm số y = f(x), ta thực hiện các bước sau:
-
Bước 1: Xác định tập xác định D của hàm số.
-
Bước 2: Tính các giới hạn sau:
- $lim_{xrightarrow +infty } f(x)$
- $lim_{xrightarrow -infty } f(x)$
-
Bước 3: Kết luận:
- Nếu $lim_{xrightarrow +infty } f(x) = y_0$, thì đường thẳng y = y₀ là tiệm cận ngang của đồ thị hàm số khi x tiến tới dương vô cực.
- Nếu $lim_{xrightarrow -infty } f(x) = y_0$, thì đường thẳng y = y₀ là tiệm cận ngang của đồ thị hàm số khi x tiến tới âm vô cực.
Ví dụ: Tìm tiệm cận ngang của đồ thị hàm số y = (x + 1) / (x² + 1).
Giải:
- Tập xác định: D = R
- Ta có: $lim_{xrightarrow +infty } y = 0$ và $lim_{xrightarrow -infty } y = 0$
- Vậy, đồ thị hàm số có một tiệm cận ngang là y = 0.
3. Công Thức Tính Nhanh Tiệm Cận Ngang
3.1. Hàm Phân Thức Hữu Tỉ
Đối với hàm phân thức hữu tỉ y = P(x) / Q(x), trong đó P(x) và Q(x) là các đa thức, ta có các trường hợp sau:
- Bậc của P(x) < Bậc của Q(x): Tiệm cận ngang là y = 0.
- Bậc của P(x) = Bậc của Q(x): Tiệm cận ngang là y = a/b, trong đó a là hệ số bậc cao nhất của P(x) và b là hệ số bậc cao nhất của Q(x).
- Bậc của P(x) > Bậc của Q(x): Không có tiệm cận ngang.
Ảnh: Bảng tóm tắt công thức nhanh để xác định tiệm cận ngang của hàm phân thức hữu tỉ dựa trên so sánh bậc của tử và mẫu thức.
3.2. Hàm Phân Thức Vô Tỉ
Đối với hàm phân thức vô tỉ, việc tìm tiệm cận ngang thường phức tạp hơn và đòi hỏi kỹ năng tính giới hạn tốt. Tuy nhiên, một số dạng thường gặp có thể áp dụng công thức hoặc biến đổi để đưa về dạng quen thuộc.
Ảnh: Bảng tóm tắt cách xác định tiệm cận ngang của một số dạng hàm phân thức vô tỉ thường gặp.
4. Sử Dụng Máy Tính Casio để Tìm Tiệm Cận Ngang
Máy tính Casio là một công cụ hữu ích để kiểm tra và tìm tiệm cận ngang một cách nhanh chóng.
- Bước 1: Nhập hàm số vào máy tính.
- Bước 2: Sử dụng chức năng CALC (hoặc SHIFT CALC) để tính giá trị của hàm số tại x rất lớn (ví dụ: x = 10^9) và x rất nhỏ (ví dụ: x = -10^9).
- Bước 3: Giá trị thu được sẽ xấp xỉ với giới hạn của hàm số khi x tiến tới vô cực.
Ví dụ: Tìm tiệm cận ngang của đồ thị hàm số y = (1 – x) / (3x + 1).
Giải:
- Nhập hàm số vào máy tính.
- Sử dụng CALC với x = 10^9, ta được kết quả xấp xỉ -0.3333…
- Sử dụng CALC với x = -10^9, ta được kết quả xấp xỉ -0.3333…
- Vậy, tiệm cận ngang của đồ thị hàm số là y = -1/3.
Ảnh: Minh họa thao tác sử dụng máy tính Casio để tính giá trị hàm số tại x rất lớn, từ đó xác định tiệm cận ngang.
5. Xác Định Tiệm Cận Ngang Từ Bảng Biến Thiên
Bảng biến thiên cung cấp thông tin trực quan về sự biến thiên của hàm số. Để tìm tiệm cận ngang từ bảng biến thiên, ta quan sát giá trị của hàm số khi x tiến tới vô cực.
- Nếu giá trị của hàm số tiến tới một số hữu hạn y₀ khi x tiến tới dương vô cực hoặc âm vô cực, thì y = y₀ là tiệm cận ngang.
6. Bài Tập Vận Dụng
Bài 1: Tìm tiệm cận ngang của đồ thị hàm số y = (x + √(4x² – 3)) / (2x + 3).
Giải:
- $lim_{xrightarrow -infty } y = lim_{xrightarrow -infty } (x + √(4x² – 3)) / (2x + 3) = -1/2$
- $lim_{xrightarrow +infty } y = lim_{xrightarrow +infty } (x + √(4x² – 3)) / (2x + 3) = 3/2$
- Vậy, y = 3/2 và y = -1/2 là các tiệm cận ngang của đồ thị hàm số.
Bài 2: Tìm tiệm cận ngang của đồ thị hàm số y = (x – 1) / √(x² – 3x + 2).
Giải:
- $lim_{xrightarrow -infty } y = lim_{xrightarrow -infty } (x – 1) / √(x² – 3x + 2) = -1$
- $lim_{xrightarrow +infty } y = lim_{xrightarrow +infty } (x – 1) / √(x² – 3x + 2) = 1$
- Vậy, y = 1 và y = -1 là các tiệm cận ngang của đồ thị hàm số.
Bài 3: Tìm giá trị của tham số m để đồ thị hàm số y = √(m² + 2x) – x có tiệm cận ngang.
Bài 4: Tìm đường tiệm cận ngang của đồ thị hàm số y = √(x² + 2x + 3) – x.
Giải:
- $lim_{xrightarrow +infty } (√(x² + 2x + 3) – x) = lim_{xrightarrow +infty } ((√(x² + 2x + 3) – x)(√(x² + 2x + 3) + x)) / (√(x² + 2x + 3) + x) = lim_{xrightarrow +infty } (2x + 3) / (√(x² + 2x + 3) + x) = 1$
- Vậy, y = 1 là tiệm cận ngang của đồ thị hàm số.
Bài 5: Tìm giá trị m để hàm số y = (mx³ – 2) / (x² – 3x + 2) có hai tiệm cận đứng.
Giải:
- x² – 3x + 2 = 0 ⇔ x = 1 hoặc x = 2
- Để hàm số có hai tiệm cận đứng, x = 1 và x = 2 không phải là nghiệm của tử số mx³ – 2.
Kết Luận
Hiểu rõ định nghĩa và nắm vững các phương pháp tìm tiệm cận ngang là chìa khóa để giải quyết các bài toán liên quan một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để chinh phục mọi dạng bài tập về tiệm cận ngang. Chúc bạn thành công!