Bảng biến thiên là công cụ quan trọng để khảo sát và vẽ đồ thị hàm số. Bài viết này sẽ hướng dẫn chi tiết Cách Làm Bảng Biến Thiên cho hàm số bậc 2, giúp bạn nắm vững kiến thức và giải quyết các bài tập liên quan.
1. Kiến Thức Tổng Quan về Hàm Số Bậc 2
Hàm số bậc hai có dạng tổng quát:
y = ax² + bx + c, với a ≠ 0.
Trong đó:
- a, b, c là các hằng số.
- Tập xác định của hàm số là D = ℝ (tập hợp tất cả các số thực).
Việc xác định hệ số a rất quan trọng để biết được hướng của đồ thị hàm số (parabol).
Alt text: Minh họa đồ thị hàm số bậc hai y=ax^2+bx+c, thể hiện parabol hướng lên hoặc xuống tùy thuộc vào dấu của hệ số a.
2. Các Bước Lập Bảng Biến Thiên Hàm Số Bậc 2
2.1. Xác định hệ số a
Hệ số a quyết định hình dạng và chiều biến thiên của hàm số.
- Nếu a > 0: Parabol hướng lên trên, hàm số nghịch biến trên khoảng (-∞; -b/2a) và đồng biến trên khoảng (-b/2a; +∞).
- Nếu a < 0: Parabol hướng xuống dưới, hàm số đồng biến trên khoảng (-∞; -b/2a) và nghịch biến trên khoảng (-b/2a; +∞).
2.2. Tìm tọa độ đỉnh của Parabol
Đỉnh I của parabol có tọa độ (xI; yI), trong đó:
- xI = -b/2a
- yI = -Δ/4a = f(xI), với Δ = b² – 4ac
2.3. Lập Bảng Biến Thiên
Dựa vào hệ số a và tọa độ đỉnh, ta lập bảng biến thiên:
-
Trường hợp a > 0:
x -∞ -b/2a +∞ y +∞ f(-b/2a) = -Δ/4a (Min) +∞ Chiều Giảm (đi xuống) Tăng (đi lên) 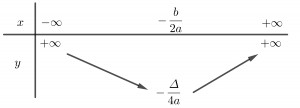
Alt text: Bảng biến thiên hàm số bậc hai với a > 0, minh họa sự nghịch biến trên khoảng (-∞; -b/2a) và đồng biến trên khoảng (-b/2a; +∞), với giá trị nhỏ nhất tại đỉnh parabol.
-
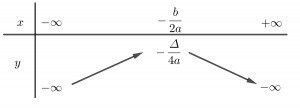
Trường hợp a < 0:
x -∞ -b/2a +∞ y -∞ f(-b/2a) = -Δ/4a (Max) -∞ Chiều Tăng (đi lên) Giảm (đi xuống) Alt text: Bảng biến thiên hàm số bậc hai với a < 0, minh họa sự đồng biến trên khoảng (-∞; -b/2a) và nghịch biến trên khoảng (-b/2a; +∞), với giá trị lớn nhất tại đỉnh parabol.
3. Ví Dụ Minh Họa
Ví dụ 1: Lập bảng biến thiên của hàm số y = x² – 4x + 3.
- a = 1 > 0
- b = -4
- c = 3
- xI = -(-4)/(2*1) = 2
- yI = 2² – 4*2 + 3 = -1
Bảng biến thiên:
| x | -∞ | 2 | +∞ |
|---|---|---|---|
| y | +∞ | -1 | +∞ |
| Chiều | Giảm | Tăng |
Ví dụ 2: Lập bảng biến thiên của hàm số y = -2x² + 8x – 6.
- a = -2 < 0
- b = 8
- c = -6
- xI = -8/(2*(-2)) = 2
- yI = -22² + 82 – 6 = 2
Bảng biến thiên:
| x | -∞ | 2 | +∞ |
|---|---|---|---|
| y | -∞ | 2 | -∞ |
| Chiều | Tăng | Giảm |
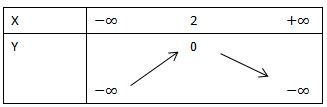
Ví dụ 3: Lập bảng biến thiên của hàm số y = -x² + 4x – 4
- a = -1 < 0
- b = 4
- c = -4
- xI = -4/(2*(-1)) = 2
- yI = -(2)² + 4*2 – 4 = 0
Bảng biến thiên:
Alt text: Bảng biến thiên của hàm số y = -x^2 + 4x – 4, với đỉnh parabol tại (2;0) và hàm số nghịch biến trên khoảng (2; +∞).
4. Ứng Dụng của Bảng Biến Thiên
Bảng biến thiên là công cụ hữu ích để:
- Xác định khoảng đồng biến và nghịch biến của hàm số.
- Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên một khoảng cho trước.
- Vẽ đồ thị hàm số một cách chính xác.
- Giải các bài toán liên quan đến biện luận số nghiệm của phương trình.
5. Bài Tập Luyện Tập
Lập bảng biến thiên của các hàm số sau:
- y = 2x² + 4x – 1
- y = -3x² + 6x + 2
- y = x² – 2x
Nắm vững cách làm bảng biến thiên hàm số bậc 2 là bước quan trọng để học tốt chương trình Toán THPT. Hãy luyện tập thường xuyên để thành thạo kỹ năng này!