Nắm vững các công thức tính chu vi và diện tích là nền tảng quan trọng trong học toán, đặc biệt là hình học. Bài viết này tổng hợp đầy đủ các công thức cơ bản, giúp học sinh dễ dàng áp dụng vào giải bài tập và ứng dụng thực tế.
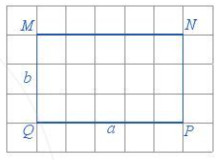
1. Hình Chữ Nhật: Chu Vi và Diện Tích
Alt: Hình chữ nhật với các cạnh và ký hiệu a, b để minh họa công thức tính chu vi diện tích.
- Chu vi: P = (a + b) x 2 (a là chiều dài, b là chiều rộng)
- Diện tích: S = a x b
2. Hình Vuông: Tính Chu Vi và Diện Tích Đơn Giản
Alt: Hình vuông cạnh a minh họa công thức tính chu vi và diện tích, tối ưu cho tìm kiếm “công thức hình vuông”.
- Chu vi: P = a x 4 (a là độ dài cạnh)
- Diện tích: S = a x a = a²
3. Hình Tam Giác: Công Thức Tính Chu Vi và Diện Tích
Alt: Hình tam giác với đáy và chiều cao, chú thích a, h, thể hiện công thức tính diện tích tam giác.
- Chu vi: P = a + b + c (a, b, c là độ dài các cạnh)
- Diện tích: S = (a x h) / 2 (a là độ dài đáy, h là chiều cao tương ứng)
4. Hình Bình Hành: Chu Vi và Diện Tích
Alt: Hình bình hành minh họa công thức tính diện tích và chu vi, tập trung vào đáy và chiều cao.
- Chu vi: P = (a + b) x 2 (a và b là độ dài hai cạnh kề)
- Diện tích: S = a x h (a là độ dài đáy, h là chiều cao tương ứng)
5. Hình Thoi: Chu Vi và Diện Tích
Alt: Hình thoi và đường chéo, thể hiện công thức diện tích hình thoi thông qua đường chéo.
- Chu vi: P = a x 4 (a là độ dài cạnh)
- Diện tích: S = (p x q) / 2 (p và q là độ dài hai đường chéo)
6. Hình Thang: Chu Vi và Diện Tích
Alt: Hình thang minh họa công thức tính diện tích với đáy lớn, đáy nhỏ và chiều cao.
- Chu vi: P = a + b + c + d (a, b là độ dài hai đáy, c và d là độ dài hai cạnh bên)
- Diện tích: S = ((a + b) x h) / 2 (a và b là độ dài hai đáy, h là chiều cao)
7. Hình Tròn: Chu Vi (Đường Tròn) và Diện Tích
Alt: Hình tròn với bán kính r, phục vụ việc học và tra cứu công thức tính diện tích hình tròn.
- Chu vi (đường tròn): C = 2 x π x r = π x d (r là bán kính, d là đường kính, π ≈ 3.14)
- Diện tích: S = π x r²
Nắm vững “Các Công Thức Tính Chu Vi Diện Tích” của các hình cơ bản này là chìa khóa để giải quyết nhiều bài toán hình học và ứng dụng trong thực tế. Hãy luyện tập thường xuyên để ghi nhớ và sử dụng thành thạo.