1. Định Nghĩa Elip
Trong mặt phẳng, cho hai điểm cố định $F_1$ và $F_2$ (gọi là các tiêu điểm). Elip là tập hợp các điểm M sao cho tổng khoảng cách từ M đến hai tiêu điểm là một hằng số: $MF_1 + MF_2 = 2a$, với $a$ là một số dương cho trước. Khoảng cách giữa hai tiêu điểm, $F_1F_2 = 2c$, được gọi là tiêu cự của elip.
2. Phương Trình Chính Tắc Của Elip
Chọn hệ trục tọa độ Oxy sao cho hai tiêu điểm nằm trên trục Ox và đối xứng qua gốc O, tức $F_1(-c; 0)$ và $F_2(c; 0)$. Khi đó, phương trình của elip có dạng:
$frac{x^2}{a^2} + frac{y^2}{b^2} = 1$
Trong đó: $b^2 = a^2 – c^2$. Phương trình này được gọi là phương trình chính tắc của elip.
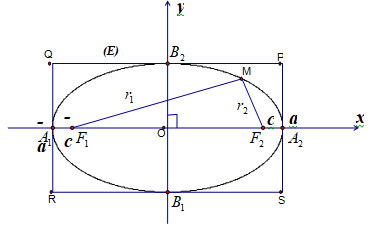
Hình ảnh minh họa phương trình chính tắc của elip, thể hiện mối quan hệ giữa các trục và tiêu điểm, giúp học sinh hình dung rõ hơn về hình dạng và các yếu tố cơ bản của elip.
Ví dụ: Viết phương trình chính tắc của elip (E) biết độ dài trục lớn bằng 10 và độ dài trục bé bằng 8.
Giải:
Ta có $2a = 10 Rightarrow a = 5$ và $2b = 8 Rightarrow b = 4$.
Vậy phương trình chính tắc của elip (E) là: $frac{x^2}{25} + frac{y^2}{16} = 1$.
3. Các Yếu Tố và Hình Dạng Của Elip
Với elip (E) có phương trình chính tắc $frac{x^2}{a^2} + frac{y^2}{b^2} = 1$, ta có các yếu tố sau:
- Tính đối xứng: Elip có hai trục đối xứng là Ox và Oy, và tâm đối xứng là gốc tọa độ O.
- Các đỉnh: Elip cắt trục Ox tại hai điểm $A_1(-a; 0)$ và $A_2(a; 0)$, và cắt trục Oy tại hai điểm $B_1(0; -b)$ và $B_2(0; b)$. Các điểm này được gọi là các đỉnh của elip.
- Trục lớn và trục bé: Đoạn thẳng $A_1A_2$ có độ dài 2a được gọi là trục lớn, và đoạn thẳng $B_1B_2$ có độ dài 2b được gọi là trục bé của elip.
Hình ảnh mô tả chi tiết các thành phần của elip, bao gồm trục lớn, trục nhỏ, tiêu điểm, và các đỉnh, giúp người học dễ dàng nhận diện và ghi nhớ các khái niệm quan trọng.
Ví dụ: Cho elip (E) có phương trình $frac{x^2}{16} + frac{y^2}{9} = 1$. Xác định độ dài các trục, tọa độ các tiêu điểm và các đỉnh.
Giải:
Ta có $a^2 = 16 Rightarrow a = 4$ và $b^2 = 9 Rightarrow b = 3$.
Suy ra $c = sqrt{a^2 – b^2} = sqrt{16 – 9} = sqrt{7}$.
Vậy:
- Độ dài trục lớn: $2a = 8$.
- Độ dài trục bé: $2b = 6$.
- Tọa độ các tiêu điểm: $F_1(-sqrt{7}; 0)$ và $F_2(sqrt{7}; 0)$.
- Tọa độ các đỉnh: $A_1(-4; 0)$, $A_2(4; 0)$, $B_1(0; -3)$, và $B_2(0; 3)$.
Hình ảnh trực quan về đồ thị elip, minh họa vị trí các đỉnh, tiêu điểm và các trục, giúp củng cố kiến thức và kỹ năng vẽ hình elip.
4. Các Dạng Bài Tập Về Phương Trình Elip và Cách Giải
Dạng 1: Xác định phương trình chính tắc của elip khi biết các yếu tố liên quan
Ví dụ 1: Elip (E) có một tiêu điểm là $F_1(-3; 0)$ và đi qua điểm A(5; 0). Viết phương trình chính tắc của (E).
Giải:
Vì A(5; 0) thuộc elip nên a = 5.
Ta có c = 3, suy ra $b^2 = a^2 – c^2 = 25 – 9 = 16$.
Vậy phương trình chính tắc của elip (E) là: $frac{x^2}{25} + frac{y^2}{16} = 1$.
Dạng 2: Tìm tọa độ điểm trên elip thỏa mãn điều kiện cho trước
Ví dụ 2: Cho elip (E): $frac{x^2}{16} + frac{y^2}{9} = 1$. Tìm điểm M trên (E) sao cho M có hoành độ bằng 2.
Giải:
Thay $x = 2$ vào phương trình elip, ta có: $frac{4}{16} + frac{y^2}{9} = 1 Rightarrow frac{y^2}{9} = frac{3}{4} Rightarrow y^2 = frac{27}{4} Rightarrow y = pm frac{3sqrt{3}}{2}$.
Vậy có hai điểm M thỏa mãn là $M_1(2; frac{3sqrt{3}}{2})$ và $M_2(2; -frac{3sqrt{3}}{2})$.
Dạng 3: Bài toán liên quan đến tiêu điểm và khoảng cách
Ví dụ 3: Cho elip (E): $frac{x^2}{25} + frac{y^2}{9} = 1$. Gọi $F_1$ và $F_2$ là hai tiêu điểm của (E). Tìm điểm M trên (E) sao cho $MF_1 + MF_2 = 8$.
Giải:
Theo định nghĩa elip, với mọi điểm M thuộc (E), ta luôn có $MF_1 + MF_2 = 2a$.
Trong trường hợp này, $a = 5$, suy ra $2a = 10$. Vậy không có điểm M nào trên (E) thỏa mãn $MF_1 + MF_2 = 8$ (vì $8 < 10$). Có lẽ có lỗi trong dữ kiện đề bài, biểu thức phải là $MF_1 + MF_2 = 10$
Dạng 4: Tìm phương trình elip khi biết tâm sai
Ví dụ 4: Viết phương trình chính tắc của elip (E), biết tâm sai $e = frac{sqrt{5}}{3}$ và độ dài trục lớn bằng 6.
Giải:
Ta có $2a = 6 Rightarrow a = 3$.
Tâm sai $e = frac{c}{a} = frac{sqrt{5}}{3} Rightarrow c = a cdot e = 3 cdot frac{sqrt{5}}{3} = sqrt{5}$.
Suy ra $b^2 = a^2 – c^2 = 9 – 5 = 4$.
Vậy phương trình chính tắc của elip (E) là: $frac{x^2}{9} + frac{y^2}{4} = 1$.
Hình ảnh mô tả một bài toán cụ thể về elip, giúp học sinh liên hệ kiến thức lý thuyết với các ứng dụng thực tế, từ đó nâng cao khả năng giải quyết vấn đề.