I. Gia Tốc Trong Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều là chuyển động mà vận tốc có độ lớn thay đổi đều theo thời gian. Có hai loại chính:
- Chuyển động thẳng nhanh dần đều: Vận tốc tăng đều theo thời gian (a.v > 0).
- Chuyển động thẳng chậm dần đều: Vận tốc giảm đều theo thời gian (a.v < 0).
Gia tốc (a) trong chuyển động thẳng biến đổi đều là đại lượng không đổi theo thời gian, thể hiện sự thay đổi vận tốc trong một đơn vị thời gian. Công thức tính gia tốc:
(a = frac{Delta v}{Delta t} = frac{v_2 – v_1}{t_2 – t_1})
Trong đó:
- (a): gia tốc (m/s²)
- (Delta v): độ biến thiên vận tốc (m/s)
- (Delta t): khoảng thời gian (s)
- (v_1): vận tốc tại thời điểm (t_1) (m/s)
- (v_2): vận tốc tại thời điểm (t_2) (m/s)
II. Vận Tốc Tức Thời Của Chuyển Động Thẳng Biến Đổi Đều
Vận tốc tức thời ((v_t)) tại một thời điểm (t) trong chuyển động thẳng biến đổi đều được xác định bởi công thức:
(v_t = v_0 + a.t)
Trong đó:
- (v_t): vận tốc tại thời điểm (t) (m/s)
- (v_0): vận tốc ban đầu (tại thời điểm (t = 0)) (m/s)
- (a): gia tốc (m/s²)
- (t): thời gian (s)
Công thức này cho thấy vận tốc thay đổi tuyến tính theo thời gian, với hệ số góc là gia tốc (a).
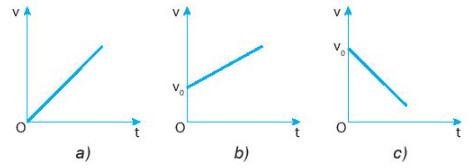
III. Đồ Thị Vận Tốc – Thời Gian (v-t)
Đồ thị vận tốc – thời gian (v-t) của chuyển động thẳng biến đổi đều là một đường thẳng.
- Đường thẳng dốc lên: Chuyển động thẳng nhanh dần đều (gia tốc dương).
- Đường thẳng dốc xuống: Chuyển động thẳng chậm dần đều (gia tốc âm).
- Độ dốc của đường thẳng: Biểu thị giá trị của gia tốc.
- Giao điểm với trục tung: Biểu thị vận tốc ban đầu (v_0).
IV. Độ Dịch Chuyển Trong Chuyển Động Thẳng Biến Đổi Đều
1. Tính Độ Dịch Chuyển Bằng Đồ Thị (v-t)
Độ dịch chuyển trong một khoảng thời gian nhất định bằng diện tích hình giới hạn bởi đồ thị vận tốc – thời gian, trục thời gian và hai đường thẳng đứng tương ứng với thời điểm đầu và cuối của khoảng thời gian đó.
- Hình chữ nhật (chuyển động thẳng đều): Diện tích = (v.t)
- Hình thang (chuyển động thẳng biến đổi đều): Diện tích = (frac{(v_0 + v_t).t}{2})
2. Tính Độ Dịch Chuyển Bằng Công Thức
Công thức tính độ dịch chuyển ((d)) trong chuyển động thẳng biến đổi đều:
(d = v_0.t + frac{1}{2}.a.t^2)
Trong đó:
- (d): độ dịch chuyển (m)
- (v_0): vận tốc ban đầu (m/s)
- (a): gia tốc (m/s²)
- (t): thời gian (s)
V. Mối Liên Hệ Giữa Vận Tốc, Gia Tốc và Độ Dịch Chuyển
Công thức liên hệ giữa vận tốc cuối ((v_t)), vận tốc đầu ((v_0)), gia tốc ((a)) và độ dịch chuyển ((d)):
(v_t^2 – v_0^2 = 2.a.d)
Công thức này hữu ích khi không biết thời gian (t).