Bài viết này sẽ giúp bạn nắm vững kiến thức về Các Cạnh Trong Tam Giác Vuông, từ đó giải quyết các bài toán hình học một cách nhanh chóng và chính xác. Chúng ta sẽ cùng tìm hiểu về định nghĩa, tính chất và các trường hợp bằng nhau liên quan đến tam giác vuông.
1. Tam Giác Vuông và Các Cạnh Đặc Biệt
Tam giác vuông là tam giác có một góc vuông (90 độ). Trong tam giác vuông, các cạnh được gọi tên như sau:
- Cạnh huyền: Là cạnh đối diện với góc vuông, và cũng là cạnh dài nhất trong tam giác vuông.
- Cạnh góc vuông: Là hai cạnh tạo thành góc vuông.
Tam giác vuông với cạnh huyền và hai cạnh góc vuông được xác định rõ ràng.
2. Các Trường Hợp Bằng Nhau Của Tam Giác Vuông Dựa Trên Các Cạnh
Việc xác định các cạnh của tam giác vuông giúp chúng ta dễ dàng chứng minh các trường hợp bằng nhau. Dưới đây là các trường hợp thường gặp:
2.1. Hai Cạnh Góc Vuông (c-g-c)
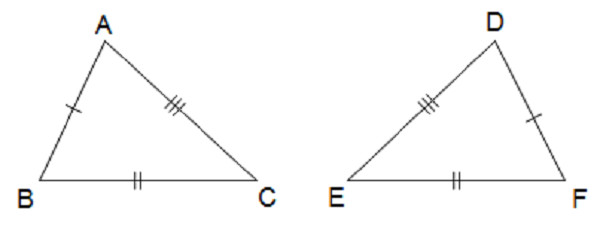
Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.
2.2. Cạnh Góc Vuông và Góc Nhọn Kề Cạnh Đó (g-c-g)
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.
2.3. Cạnh Huyền và Góc Nhọn (cạnh huyền – góc nhọn)
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.
Hai tam giác vuông có cạnh huyền và một góc nhọn tương ứng bằng nhau thì bằng nhau.
2.4. Cạnh Huyền và Cạnh Góc Vuông (cạnh huyền – cạnh góc vuông)
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.
Hai tam giác vuông có cạnh huyền và một cạnh góc vuông tương ứng bằng nhau thì bằng nhau.
3. Ứng Dụng Các Trường Hợp Bằng Nhau Của Tam Giác Vuông
Việc nắm vững các cạnh trong tam giác vuông và các trường hợp bằng nhau giúp giải quyết nhiều bài toán hình học, bao gồm:
- Chứng minh hai đoạn thẳng bằng nhau: Thông qua việc chứng minh hai tam giác vuông chứa hai đoạn thẳng đó bằng nhau.
- Chứng minh hai góc bằng nhau: Tương tự như chứng minh đoạn thẳng, sử dụng hai tam giác vuông bằng nhau để suy ra các góc tương ứng bằng nhau.
- Tìm điều kiện để hai tam giác vuông bằng nhau: Dựa vào các trường hợp bằng nhau để xác định các yếu tố cần thiết.
4. Bài Tập Vận Dụng
Ví dụ: Cho tam giác ABC vuông tại A, đường cao AH. Trên tia đối của tia HA lấy điểm D sao cho HD = HA. Chứng minh rằng tam giác BCD vuông.
Hướng dẫn:
- Xét tam giác ABH và tam giác DBH, chứng minh hai tam giác này bằng nhau (c-g-c).
- Suy ra góc ABH = góc DBH.
- Chứng minh tương tự với tam giác ACH và tam giác DCH.
- Từ đó suy ra góc CBD + góc BCD = 90 độ. Vậy tam giác BCD vuông tại D.
Bài viết này đã cung cấp kiến thức cơ bản về các cạnh trong tam giác vuông và các trường hợp bằng nhau quan trọng. Hy vọng bạn sẽ áp dụng thành công vào việc giải các bài toán hình học.