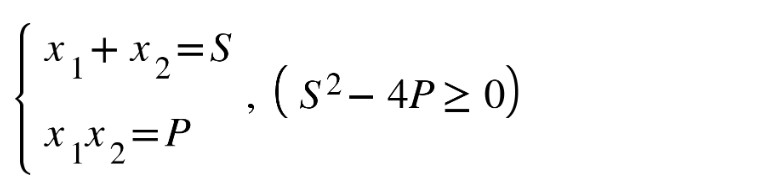Hệ thức Viète là một công cụ mạnh mẽ trong toán học, đặc biệt khi giải các bài toán liên quan đến phương trình bậc hai. Bài viết này sẽ đi sâu vào ứng dụng của hệ thức Viète trong việc biến đổi và tìm mối liên hệ giữa các nghiệm x1 và x2 của phương trình bậc hai, đồng thời cung cấp các ví dụ minh họa chi tiết và tối ưu SEO cho người đọc Việt Nam.
Hệ Thức Viète: Nền Tảng Quan Trọng
Hệ thức Viète, được đặt theo tên nhà toán học François Viète, mô tả mối quan hệ giữa các nghiệm của một phương trình đa thức và các hệ số của nó. Đối với phương trình bậc hai, hệ thức Viète cho phép chúng ta tính tổng và tích của các nghiệm mà không cần giải phương trình.
Hệ Thức Viète Thuận
Cho phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x1 và x2. Khi đó:
- Tổng hai nghiệm: x1 + x2 = -b/a
- Tích hai nghiệm: x1 * x2 = c/a
Hệ Thức Viète Đảo
Nếu hai số thực x1 và x2 thỏa mãn:
- x1 + x2 = S
- x1 * x2 = P
Thì x1 và x2 là nghiệm của phương trình bậc hai: x² – Sx + P = 0
Lưu ý: Điều kiện cần để phương trình có nghiệm là S² – 4P ≥ 0.
Các Dạng Bài Tập Biến Đổi x1-x2 Thường Gặp
Hệ thức Viète không chỉ giúp tìm nghiệm mà còn là công cụ đắc lực để biến đổi và tìm mối liên hệ giữa x1 và x2. Dưới đây là một số dạng bài tập thường gặp.
Dạng 1: Tính Giá Trị Biểu Thức Chứa x1, x2
Khi phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x1 và x2, ta có thể biểu diễn các biểu thức đối xứng giữa các nghiệm thông qua S = x1 + x2 và P = x1.x2. Ví dụ:
- x1² + x2² = (x1 + x2)² – 2x1x2 = S² – 2P
- (x1 – x2)² = (x1 + x2)² – 4x1x2 = S² – 4P
Ví dụ: Cho phương trình x² – 5x + 6 = 0 có hai nghiệm x1 và x2. Tính giá trị của biểu thức A = x1² + x2².
Lời giải:
Áp dụng hệ thức Viète, ta có:
- S = x1 + x2 = 5
- P = x1 * x2 = 6
Khi đó, A = x1² + x2² = S² – 2P = 5² – 2 * 6 = 25 – 12 = 13
Dạng 2: Tìm Điều Kiện Tham Số Để Nghiệm Thỏa Mãn Điều Kiện Cho Trước
Đây là dạng bài tập phổ biến, yêu cầu tìm giá trị của tham số để các nghiệm x1 và x2 thỏa mãn một điều kiện nào đó, ví dụ: x1 – x2 = 4, x1² + x2² = 10, hoặc một biểu thức phức tạp hơn.
Ví dụ: Cho phương trình x² – 6x + m = 0. Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn điều kiện: x1 – x2 = 4.
Lời giải:
Để phương trình có hai nghiệm phân biệt, Δ > 0, tức là (-6)² – 4m > 0 => m < 9.
Áp dụng hệ thức Viète, ta có:
- x1 + x2 = 6
- x1 * x2 = m
Kết hợp với điều kiện x1 – x2 = 4, ta có hệ phương trình:
- x1 + x2 = 6
- x1 – x2 = 4
Giải hệ phương trình, ta được x1 = 5 và x2 = 1. Thay vào x1 * x2 = m, ta có m = 5.
Kiểm tra điều kiện m < 9, ta thấy m = 5 thỏa mãn. Vậy m = 5 là giá trị cần tìm.
Dạng 3: Lập Phương Trình Bậc Hai Khi Biết Nghiệm Hoặc Mối Liên Hệ Giữa Nghiệm
Nếu biết hai nghiệm x1 và x2, ta có thể lập phương trình bậc hai bằng cách sử dụng hệ thức Viète đảo: x² – (x1 + x2)x + x1 * x2 = 0
Hoặc, nếu biết mối liên hệ giữa hai nghiệm, ta cần tìm tổng và tích của hai nghiệm đó rồi áp dụng hệ thức Viète đảo.
Dạng 4: Tìm Hệ Thức Liên Hệ Giữa Nghiệm Không Phụ Thuộc Tham Số
Trong một số bài toán, yêu cầu là tìm một hệ thức giữa x1 và x2 mà không phụ thuộc vào giá trị của tham số. Để giải quyết dạng bài này, ta thường biểu diễn x1 và x2 qua tham số, sau đó loại bỏ tham số để thu được hệ thức cần tìm.
Các Dạng Toán Nâng Cao
Ngoài các dạng cơ bản, hệ thức Viète còn được ứng dụng trong nhiều bài toán phức tạp hơn, như:
- Xét dấu nghiệm của phương trình bậc hai.
- So sánh nghiệm với một số cho trước.
- Giải các bài toán cực trị.
- Ứng dụng trong hình học giải tích.
Kết Luận
Hệ thức Viète là một công cụ không thể thiếu khi giải các bài toán liên quan đến phương trình bậc hai. Việc nắm vững lý thuyết và luyện tập các dạng bài tập khác nhau sẽ giúp học sinh tự tin hơn khi đối mặt với các bài toán khó trong chương trình học và các kỳ thi quan trọng. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về ứng dụng của hệ thức Viète trong việc biến đổi và tìm mối liên hệ giữa các nghiệm x1 và x2.