Trong lý thuyết xác suất, hai khái niệm quan trọng là biến cố xung khắc và biến cố độc lập. Hiểu rõ sự khác biệt và mối liên hệ giữa chúng là nền tảng để giải quyết các bài toán liên quan đến xác suất một cách chính xác. Bài viết này sẽ trình bày chi tiết về hai loại biến cố này, kèm theo ví dụ minh họa và các quy tắc tính xác suất liên quan.
1. Biến Cố Hợp và Giao
Để hiểu rõ hơn về biến cố xung khắc, ta cần nắm vững khái niệm biến cố hợp và biến cố giao.
a) Biến cố hợp:
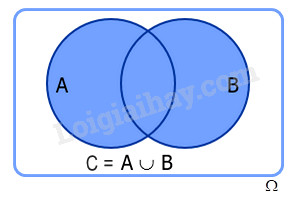
Cho hai biến cố A và B trong cùng một không gian mẫu. Biến cố hợp của A và B, ký hiệu là (A cup B), là biến cố xảy ra khi ít nhất một trong hai biến cố A hoặc B xảy ra. Nói cách khác, (A cup B) bao gồm tất cả các kết quả thuộc A hoặc thuộc B hoặc thuộc cả hai.
Alt text: Biểu đồ Venn minh họa biến cố hợp của hai tập hợp A và B, trong đó vùng tô đậm biểu thị tất cả các phần tử thuộc A hoặc B.
b) Biến cố giao:
Cho hai biến cố A và B trong cùng một không gian mẫu. Biến cố giao của A và B, ký hiệu là (A cap B) (hoặc AB), là biến cố xảy ra khi cả hai biến cố A và B đồng thời xảy ra. Nói cách khác, (A cap B) bao gồm các kết quả thuộc cả A và B.
Alt text: Biểu đồ Venn minh họa biến cố giao của hai tập hợp A và B, vùng giao nhau được tô đậm thể hiện các phần tử chung của cả hai.
2. Biến Cố Xung Khắc
Hai biến cố A và B được gọi là xung khắc nếu chúng không thể xảy ra đồng thời. Nói cách khác, nếu biến cố A xảy ra thì biến cố B không thể xảy ra, và ngược lại. Về mặt tập hợp, điều này có nghĩa là giao của hai biến cố là tập rỗng: (A cap B = emptyset).
Alt text: Biểu đồ Venn thể hiện hai biến cố A và B xung khắc, không có phần tử chung, minh họa bằng hai hình tròn rời nhau.
Ví dụ:
- Khi tung một đồng xu, biến cố “mặt sấp” và biến cố “mặt ngửa” là hai biến cố xung khắc.
- Khi gieo một con xúc xắc, biến cố “xuất hiện mặt chẵn” và biến cố “xuất hiện mặt lẻ” là hai biến cố xung khắc.
3. Biến Cố Độc Lập
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia.
Ví dụ:
- Tung hai đồng xu cùng một lúc. Kết quả của đồng xu thứ nhất không ảnh hưởng đến kết quả của đồng xu thứ hai.
- Chọn ngẫu nhiên một học sinh từ một lớp và chọn ngẫu nhiên một học sinh từ một lớp khác. Việc chọn học sinh từ lớp này không ảnh hưởng đến việc chọn học sinh từ lớp kia.
Lưu ý quan trọng:
- Nếu A và B là hai biến cố độc lập, thì các cặp biến cố sau cũng độc lập: A và (overline{B}), (overline{A}) và B, (overline{A}) và (overline{B}), trong đó (overline{A}) và (overline{B}) là biến cố đối của A và B, tương ứng.
4. Phân Biệt Biến Cố Xung Khắc và Độc Lập
Đây là hai khái niệm dễ gây nhầm lẫn. Điểm khác biệt chính là:
- Xung khắc: Hai biến cố không thể xảy ra đồng thời.
- Độc lập: Việc xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia.
Hai biến cố không thể vừa xung khắc vừa độc lập (ngoại trừ trường hợp một trong hai biến cố có xác suất bằng 0). Nếu hai biến cố xung khắc (và có xác suất khác 0), thì chúng phụ thuộc nhau vì nếu một biến cố xảy ra, biến cố kia chắc chắn không xảy ra.
5. Các Quy Tắc Tính Xác Suất
a) Công thức cộng xác suất:
Cho hai biến cố A và B bất kỳ, xác suất để ít nhất một trong hai biến cố xảy ra được tính theo công thức:
(P(A cup B) = P(A) + P(B) – P(A cap B))
Nếu A và B là hai biến cố xung khắc, thì (P(A cap B) = 0), do đó công thức trở thành:
(P(A cup B) = P(A) + P(B))
b) Công thức nhân xác suất:
Cho hai biến cố A và B. Nếu A và B là hai biến cố độc lập, thì xác suất để cả hai biến cố cùng xảy ra được tính theo công thức:
(P(A cap B) = P(A) cdot P(B))
Alt text: Hình ảnh công thức tính xác suất P(A và B) bằng P(A) nhân P(B) khi A và B là hai biến cố độc lập, thể hiện mối liên hệ giữa các xác suất.
6. Ứng Dụng và Bài Tập
Hiểu rõ về Biến Cố Xung Khắc Và độc Lập giúp ta giải quyết nhiều bài toán thực tế. Dưới đây là một số ví dụ:
Ví dụ 1: Một hộp có 5 bi đỏ và 3 bi xanh. Lấy ngẫu nhiên 2 bi. Tính xác suất để lấy được 1 bi đỏ và 1 bi xanh trong hai trường hợp:
- Lấy có hoàn lại (sau khi lấy bi thứ nhất thì trả lại hộp)
- Lấy không hoàn lại (sau khi lấy bi thứ nhất thì không trả lại hộp)
Giải:
- Lấy có hoàn lại: Hai lần lấy bi là độc lập.
- P(lấy bi đỏ trước, bi xanh sau) = (5/8) * (3/8) = 15/64
- P(lấy bi xanh trước, bi đỏ sau) = (3/8) * (5/8) = 15/64
- P(lấy được 1 bi đỏ và 1 bi xanh) = 15/64 + 15/64 = 30/64 = 15/32
- Lấy không hoàn lại: Hai lần lấy bi là không độc lập.
- P(lấy bi đỏ trước, bi xanh sau) = (5/8) * (3/7) = 15/56
- P(lấy bi xanh trước, bi đỏ sau) = (3/8) * (5/7) = 15/56
- P(lấy được 1 bi đỏ và 1 bi xanh) = 15/56 + 15/56 = 30/56 = 15/28
Ví dụ 2: Một hệ thống báo động có hai cảm biến hoạt động độc lập. Xác suất để cảm biến thứ nhất báo động khi có sự cố là 0.9, xác suất để cảm biến thứ hai báo động khi có sự cố là 0.8. Tính xác suất để hệ thống báo động khi có sự cố.
Giải:
Gọi A là biến cố “cảm biến thứ nhất báo động” và B là biến cố “cảm biến thứ hai báo động”.
Hệ thống báo động khi có ít nhất một cảm biến báo động, tức là biến cố (A cup B) xảy ra.
Vì A và B độc lập, ta có:
(P(A cup B) = P(A) + P(B) – P(A cap B) = P(A) + P(B) – P(A) cdot P(B))
(P(A cup B) = 0.9 + 0.8 – 0.9 * 0.8 = 0.9 + 0.8 – 0.72 = 0.98)
Vậy xác suất để hệ thống báo động khi có sự cố là 0.98.
Nắm vững các khái niệm và quy tắc về biến cố xung khắc và độc lập là rất quan trọng để giải quyết các bài toán xác suất và thống kê một cách hiệu quả. Hy vọng bài viết này cung cấp cho bạn một cái nhìn tổng quan và sâu sắc về chủ đề này.