Hàm số bậc hai là một trong những khái niệm quan trọng trong chương trình toán học phổ thông. Bài viết này sẽ đi sâu vào lý thuyết và các dạng bài tập liên quan, đặc biệt tập trung vào trường hợp “Bề Lõm Hướng Lên” của đồ thị hàm số.
1. Khái Niệm Hàm Số Bậc Hai
Hàm số bậc hai có dạng tổng quát như sau:
$y = ax^2 + bx + c$
Trong đó:
- $a, b, c$ là các hằng số và $a neq 0$.
- Tập xác định của hàm số là tập số thực R.
- Đồ thị của hàm số bậc hai là một đường parabol.
2. Chiều Biến Thiên và Bề Lõm của Parabol
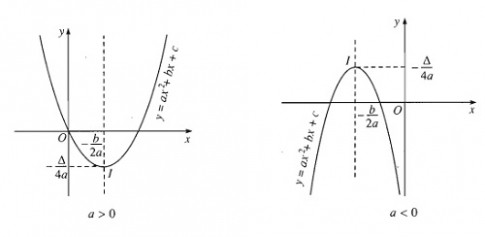
Chiều biến thiên của hàm số bậc hai phụ thuộc vào dấu của hệ số $a$. Đặc biệt, dấu của $a$ quyết định “bề lõm” của parabol quay lên hay xuống.
-
Trường hợp $a > 0$ (Bề Lõm Hướng Lên):
- Hàm số nghịch biến trên khoảng $(-infty, -frac{b}{2a})$.
- Hàm số đồng biến trên khoảng $(-frac{b}{2a}, +infty)$.
- Hàm số đạt giá trị nhỏ nhất (GTNN) là $-frac{Delta}{4a}$ tại $x = -frac{b}{2a}$.
- Parabol có bề lõm hướng lên trên, với đỉnh là điểm thấp nhất.
-
Trường hợp $a < 0$:
- Hàm số đồng biến trên khoảng $(-infty, -frac{b}{2a})$.
- Hàm số nghịch biến trên khoảng $(-frac{b}{2a}, +infty)$.
- Hàm số đạt giá trị lớn nhất (GTLN) là $-frac{Delta}{4a}$ tại $x = -frac{b}{2a}$.
- Parabol có bề lõm hướng xuống dưới, với đỉnh là điểm cao nhất.
3. Vẽ Đồ Thị Hàm Số Bậc Hai và Xác Định Bề Lõm
Để vẽ đồ thị hàm số bậc hai $y = ax^2 + bx + c$, ta thực hiện các bước sau:
- Xác định tọa độ đỉnh $I(-frac{b}{2a}, -frac{Delta}{4a})$: Đỉnh là điểm quan trọng nhất của parabol.
- Xác định trục đối xứng $x = -frac{b}{2a}$: Parabol đối xứng qua đường thẳng này.
- Xác định hướng bề lõm:
- Nếu $a > 0$, bề lõm hướng lên.
- Nếu $a < 0$, bề lõm hướng xuống.
- Tìm một số điểm thuộc đồ thị: Chọn các giá trị $x$ dễ tính toán và tìm giá trị $y$ tương ứng. Đặc biệt, nên tìm giao điểm của parabol với các trục tọa độ (nếu có).
- Vẽ parabol: Sử dụng các thông tin đã tìm được để vẽ đường parabol.
4. Bài Tập Vận Dụng
Bài tập 1: Cho hàm số $y = 2x^2 – 4x + 1$.
a) Xác định tọa độ đỉnh và trục đối xứng của parabol.
b) Vẽ đồ thị hàm số.
c) Xác định khoảng đồng biến và nghịch biến của hàm số.
Giải:
a) Ta có $a = 2, b = -4, c = 1$.
Tọa độ đỉnh: $I(-frac{b}{2a}, -frac{Delta}{4a}) = I(1, -1)$.
Trục đối xứng: $x = -frac{b}{2a} = 1$.
b) Đồ thị hàm số: Vì $a = 2 > 0$, parabol có bề lõm hướng lên. Ta tìm thêm một vài điểm thuộc đồ thị, ví dụ: $(0, 1), (2, 1)$.
c) Khoảng đồng biến: $(1, +infty)$.
Khoảng nghịch biến: $(-infty, 1)$.
Bài tập 2: Tìm $m$ để hàm số $y = (m-1)x^2 + 2mx + m + 3$ có bề lõm hướng lên và đạt giá trị nhỏ nhất bằng -2.
Giải:
Để hàm số có bề lõm hướng lên, ta cần $m – 1 > 0 Leftrightarrow m > 1$.
Giá trị nhỏ nhất đạt được tại $x = -frac{b}{2a} = -frac{2m}{2(m-1)} = -frac{m}{m-1}$.
Giá trị nhỏ nhất là: $y = -frac{Delta}{4a} = -2$.
Tính $Delta = (2m)^2 – 4(m-1)(m+3) = 4m^2 – 4(m^2 + 2m – 3) = -8m + 12$.
Vậy $-frac{-8m + 12}{4(m-1)} = -2 Leftrightarrow -8m + 12 = 8(m-1) Leftrightarrow -8m + 12 = 8m – 8 Leftrightarrow 16m = 20 Leftrightarrow m = frac{5}{4}$.
Giá trị $m = frac{5}{4}$ thỏa mãn điều kiện $m > 1$.
Bài tập 3: Xác định parabol (P) $y=ax^{2}+bx+c$, $aneq 0$ biết (P) đi qua M(4;3) cắt Ox tại N(3;0) và P sao cho $Delta INP$ có diện tích bằng 1 biết hoành độ điểm P nhỏ hơn 3.
5. Kết Luận
Hiểu rõ về hàm số bậc hai, đặc biệt là trường hợp “bề lõm hướng lên” ($a > 0$) sẽ giúp bạn giải quyết nhiều bài toán liên quan đến đồ thị, cực trị và ứng dụng thực tế. Hãy luyện tập thường xuyên để nắm vững kiến thức này.