1. Phương pháp xác định giao điểm
Để tìm giao điểm của đường thẳng $d$ và mặt phẳng $(alpha)$, ta thường thực hiện theo các bước sau:
- Chọn một mặt phẳng $(beta)$ chứa đường thẳng $d$. Việc chọn $(beta)$ sao cho dễ dàng xác định giao tuyến với $(alpha)$ là rất quan trọng.
- Tìm giao tuyến $c$ của hai mặt phẳng $(alpha)$ và $(beta)$. Giao tuyến này là tập hợp các điểm chung của hai mặt phẳng. Lưu ý: Xem thêm các phương pháp xác định giao tuyến của hai mặt phẳng.
- Tìm giao điểm $A$ của hai đường thẳng $d$ và $c$. Điểm $A$ này chính là giao điểm cần tìm của đường thẳng $d$ và mặt phẳng $(alpha)$.
2. Các ví dụ minh họa chi tiết
Ví dụ 1: Cho tứ giác $ABCD$ có $AB$ không song song với $CD$. Gọi $S$ là điểm nằm ngoài mặt phẳng $(ABCD)$, $M$ là trung điểm của $SC$. Tìm giao điểm $N$ của đường thẳng $SD$ và mặt phẳng $(MAB)$.
Lời giải:
Trên mặt phẳng $(SAC)$, gọi $I = AM cap SO$.
Xét mặt phẳng $(SBD)$ chứa $SD$. Ta có $(SBD) cap (MAB) = BI$.
Trên mặt phẳng $(SBD)$, gọi $N = BI cap SD$ thì $N = SD cap (MAB)$.
Ví dụ 2: Cho tứ diện $ABCD$. Lấy hai điểm $M$, $N$ lần lượt trên $AC$ và $AD$ sao cho $MN$ không song song $CD$. Lấy điểm $O$ bên trong tam giác $ΔBCD$.
a) Tìm giao tuyến của hai mặt phẳng $(OMN)$ và $(BCD)$.
b) Tìm giao điểm của các đường thẳng $BC$, $BD$ với mặt phẳng $(OMN)$.
Lời giải:
a) Trong mặt phẳng $(ACD)$ gọi $I$ là giao điểm của hai đường thẳng $NM$ và $CD$. Hiển nhiên $OI = (OMN) cap (BCD)$.
b) Trong mặt phẳng $(BCD)$ gọi $H$, $K$ là giao điểm của $OI$ với $BC$, $BD$. $K, H in OI Rightarrow K, H in (OMN)$. Vậy $H = BC cap (OMN)$, $K = BD cap (OMN)$.
Ví dụ 3: Cho hình chóp $S.ABCD$. Lấy điểm $M$ trên cạnh $SC$.
a) Tìm giao điểm của đường thẳng $AM$ và mặt phẳng $(SBD)$.
b) Lấy điểm $N$ trên cạnh $BC$. Tìm giao điểm của đường thẳng $SD$ và mặt phẳng $(AMN)$.
Lời giải:
a) Xét mặt phẳng phụ $(SAC)$ chứa $AM$. Trong mặt phẳng $(ABCD)$ gọi $O$ là giao điểm của hai đường thẳng $BD$ và $AC$ thì $SO = (SAC) cap (SBD)$. Trong mặt phẳng $(SAC)$ gọi $I$ là giao điểm của hai đường thẳng $SO$ và $AM$ thì $I = AM cap (SBD)$.
b) Xét mặt phẳng phụ $(SBD)$ chứa $SD$. Trong mặt phẳng $(ABCD)$ gọi $Y$ là giao điểm của hai đường thẳng $BD$ và $AN$ thì $IY = (SBD) cap (AMN)$. Trong mặt phẳng $(SBD)$ gọi $K$ là giao điểm của hai đường thẳng $IY$ và $SD$ thì $K = SD cap (AMN)$.
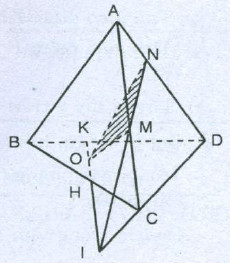
Ví dụ 4: Cho tứ diện $ABCD$. Gọi $I$ và $K$ lần lượt là hai điểm trong của các tam giác $ABC$ và $BCD$. Giả sử $IK$ cắt mặt phẳng $(ACD)$ tại $H$. Tìm $H$.
Lời giải:
Xét mặt phẳng $(BIK)$ chứa $IK$.
Trong mặt phẳng $(ABC)$: $BI$ cắt $AC$ tại $M$.
Trong mặt phẳng $(BCD)$: $BK$ cắt $CD$ tại $N$ thì $MN = (BIK) cap (ACD)$.
Trong mặt phẳng $(BIK)$, giả sử $IK$ cắt $MN$ tại $H$ thì $H$ chính là giao điểm của $IK$ và mặt phẳng $(ACD)$.
Ví dụ 5: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M$ là trung điểm $SC$.
a) Tìm giao điểm $I$ của đường thẳng $AM$ và mặt phẳng $(SBD)$. Chứng minh $IA = 2IM$.
b) Tìm giao điểm $F$ của đường thẳng $SD$ và mặt phẳng $(ABM)$. Chứng minh $F$ là trung điểm của $SD$.
c) Lấy điểm $N$ tùy ý trên cạnh $AB$. Tìm giao điểm của đường thẳng $MN$ và mặt phẳng $(SBD)$.
Lời giải:
a) Gọi $O$ là tâm hình bình hành $ABCD$. Trong mặt phẳng $(SAC)$, $AM$ cắt $SO$ tại $I$ thì $I$ là giao điểm của $AM$ và mặt phẳng $(SBD)$. Do $I$ là trọng tâm tam giác $ΔSAC$ nên $IA = 2IM$.
b) Xét mặt phẳng $(SBD)$ chứa $SD$ thì $BI$ là giao tuyến của mặt phẳng $(SBD)$ và mặt phẳng $(ABM)$. Trong mặt phẳng $(SBD)$, $BI$ cắt $SD$ tại $F$ thì $F = SD cap (ABM)$. Do $I$ cũng là trọng tâm $ΔSBD$ nên $F$ là trung điểm $SD$.
c) Xét mặt phẳng $(MAB)$ chứa $MN$ thì $BI$ là giao tuyến của mặt phẳng $(MAB)$ và mặt phẳng $(SBD)$. Trong mặt phẳng $(MAB)$, $MN$ cắt $BI$ tại $J$ thì $J$ là giao điểm của $MN$ và mặt phẳng $(SBD)$.
Ví dụ 6: Cho tứ diện $ABCD$. Gọi $M$, $N$ lần lượt là trung điểm của $AC$ và $BC$. Trên đoạn $BD$ lấy điểm $K$ sao cho $BK = 2KD$.
a) Tìm giao điểm của đường thẳng $CD$ và mặt phẳng $(MNK)$.
b) Tìm giao tuyến của hai mặt phẳng $(MNK)$ và $(ABD)$.
Lời giải:
a) Xét mặt phẳng $(BCD)$ chứa $CD$. Do $NK$ không song song với $CD$ nên $NK$ cắt $CD$ tại $I$. $I in NK Rightarrow I in (MNK)$. Vậy $CD$ cắt $(MNK)$ tại $I$.
b) Trong mặt phẳng $(ACD)$, $MI$ cắt $AD$ tại $E$. Ta có $K in BD Rightarrow K in (ABD)$ và $K in (MNK)$. Mặt khác: $E in AD Rightarrow E in (ABD)$, $E in MI Rightarrow E in (MNK)$. Vậy $EK = (MNK) cap (ABD)$. Lưu ý: $I in NK$ nên $I in (MNK)$. Do đó $MI in (MNK)$.
Ví dụ 7: Cho tứ diện $ABCD$. Gọi $I$, $J$ là trung điểm của $AC$ và $BC$. Trên $BD$ lấy điểm $K$ sao cho $BK = 2KD$.
a) Tìm giao điểm $E$ của đường thẳng $CD$ và mặt phẳng $(IJK)$.
b) Tìm giao điểm $F$ của đường thẳng $AD$ và mặt phẳng $(IJK)$.
c) Lấy $M$, $N$ trên $AB$, $CD$. Tìm giao điểm của đường thẳng $MN$ và mặt phẳng $(IJK)$.
Lời giải:
a) Trong mặt phẳng $(BCD)$ gọi $E$ là giao điểm của $CD$ và $KJ$ thì $E = CD cap (IJK)$.
b) Trong mặt phẳng $(ACD)$ gọi $F$ là giao điểm của $EI$ và $AD$. $F in EI Rightarrow F in (IJK)$. Vậy $F = AD cap (IJK)$.
c) Trong mặt phẳng $(DAC)$ gọi $A’$ là giao điểm của $AN$ và $IF$. Trong mặt phẳng $(DBC)$ gọi $B’$ là giao điểm của $BN$ và $KJ$. Trong mặt phẳng $(NAB)$ gọi $P$ là giao điểm của $A’B’$ và $MN$. Do $P in A’B’$ nên $P in (IJK)$. Vậy $MN cap (IJK) = P$.
Ví dụ 8: Cho hình chóp $S.ABCD$ có đáy hình thang đáy lớn $AB$. Lấy $I$, $Y$, $K$ lần lượt trên $SA$, $AB$, $BC$. Tìm giao điểm của:
a) $IK$ và $(SBD)$.
b) $SD$ và $(IYK)$.
c) $SC$ và $(IYK)$.
Lời giải:
a) Xét mặt phẳng $(SKA)$ chứa $KI$. Trong $(ABDC)$ gọi $H$ là giao điểm của $AK$ và $BD$ thì $SH = (SKA) cap (SBD)$. Trong mặt phẳng $(SAK)$ gọi $P$ là giao điểm của $SH$ và $IK$ thì $P = IK cap (SBD)$.
b) Xét mặt phẳng $(SAD)$ chứa $SD$. Trong mặt phẳng $(ABCD)$ gọi $Q$ là giao điểm của $YK$ và $AD$ thì $IQ = (SAD) cap (IYK)$. Trong mặt phẳng $(SAD)$ gọi $M$ là giao điểm của $QI$ và $SD$ thì $M = SD cap (IYK)$.
c) Xét mặt phẳng $(SBC)$ chứa $SC$. Trong mặt phẳng $(SAB)$ gọi $N$ là giao điểm của $IY$ và $SB$ thì $KN = (SBC) cap (IYK)$. Trong mặt phẳng $(SBC)$ gọi $R$ là giao điểm của $NK$ và $SC$ thì $N = SC cap (IYK)$.
Ví dụ 9: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$. Gọi $M$ là trung điểm $SB$, $G$ là trọng tâm tam giác $ΔSAD$.
a) Tìm giao điểm $I$ của đường thẳng $MG$ và mặt phẳng $(ABCD)$. Chứng minh $IC = 2ID$.
b) Tìm giao điểm $J$ của đường thẳng $AD$ và mặt phẳng $(OMG)$. Tính tỉ số $frac{JA}{JD}$.
c) Tìm giao điểm $K$ của đường thẳng $SA$ và mặt phẳng $(OMG)$.
Lời giải:
a) Gọi $H$ và $N$ lần lượt là trung điểm của $AD$ và $SA$. Trên mặt phẳng $(ABCD)$, $BH$ cắt $CD$ tại $I$. Trên mặt phẳng $(SBH)$, $MG$ cắt $BH$ tại $I$ thì $I$ là giao điểm của $MG$ và mặt phẳng $(ABCD)$. Ta có: $I in GM$ nên $I in (MN, CD)$. $I in BH$ nên $I in (ABCD)$. Mà giao tuyến của mặt phẳng $(MN, CD)$ và mặt phẳng $(ABCD)$ là $CD$ nên $I in CD$. Do $HD$ là đường trung bình của tam giác $ΔIBC$ nên $IC = 2ID$.
b) Xét mặt phẳng $(ABCD)$ chứa $AD$. Ta có $OI$ là giao tuyến của mặt phẳng $(OMG)$ và mặt phẳng $(ABCD)$. Trên mặt phẳng $(ABCD)$, $OI$ cắt $AD$ tại $J$ thì $J$ là giao điểm của $AD$ và mặt phẳng $(OMG)$. Tam giác $ΔAIC$ có $IO$ và $AD$ là hai đường trung tuyến nên $J$ là trọng tâm $ΔAIC$. Vậy $frac{JA}{JD} = 2$.
c) Xét mặt phẳng $(SDA)$ chứa $SA$ thì $GJ$ là giao tuyến của mặt phẳng $(SAD)$ và mặt phẳng $(OMG)$. Trong mặt phẳng $(SAD)$, $GJ$ cắt $SA$ tại $K$ thì $K = SA cap (OMG)$.
3. Bài tập tự luyện
1. Cho tứ diện $ABCD$. Trên $AC$ và $AD$ lấy hai điểm $M$, $N$ sao cho $MN$ không song song với $CD$. Gọi $I$ là điểm bên trong tam giác $ΔBCD$.
a) Tìm giao tuyến của $(IMN)$ và $(BCD)$.
b) Tìm giao điểm của $BC$ và $BD$ với $(IMN)$.
2. Cho hình chóp $S.ABCD$. Lấy điểm $M$ trên $SC$, $N$ trên $BC$. Tìm giao điểm của:
a) $AM$ và $(SBD)$.
b) $SD$ và $(AMN)$.
3. Cho tứ diện $ABCD$. Lấy điểm $M$, $N$ trên $AC$, $AD$. Lấy $O$ là điểm bên trong tam giác $ΔBCD$. Tìm giao điểm của:
a) $MN$ và $(BCD)$.
b) $OA$ và $(BMN)$.
4. Cho tứ diện $ABCD$. Lấy $I$, $J$ là hai điểm bên trong $ΔABC$ và $ΔABD$, $M$ là điểm trên $CD$. Tìm giao điểm của $IJ$ và $(ABM)$.
5. Cho hình chóp $S.ABCD$ có $AD$ không song song với $BC$. Lấy $K$ trên đoạn $SB$. Tìm giao điểm của:
a) $BC$ và $(SAD)$.
b) $SC$ và $(AKD)$.
6. Cho tứ diện $S.ABC$. Gọi $I$, $H$ là trung điểm của $SA$, $AB$. Trên $SC$ lấy điểm $K$ sao cho $CK = 3KS$.
a) Tìm giao điểm của $BC$ và $(IHK)$.
b) Gọi $M$ là trung điểm của $IH$. Tìm giao điểm của $KM$ và $(ABC)$.